题目内容
8.满足条件|z-i|+|z+i|=3的复数z在复平面上对应点的轨迹是( )| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
分析 转化复数方程为复平面点的几何意义,然后判断轨迹即可
解答 解:|z-i|+|z+i|=3的几何意义是:复数z在复平面上对应点到(0,1)与(0,-1)的距离之和为3,而且两点之间的距离为2,所以距离之和大于两点的距离,所以z的轨迹满足椭圆的定义.
故选:D.
点评 本题考查复数模的几何意义以及轨迹的判断,椭圆的定义的应用,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于( )
| A. | $\frac{4}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
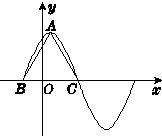 函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.