题目内容
已知定义在R上的单调递增函数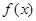 满足
满足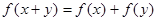 ,且
,且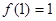 。
。
(Ⅰ)判断函数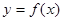 的奇偶性并证明之;
的奇偶性并证明之;
(Ⅱ)解关于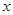 的不等式:
的不等式: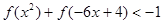 ;
;
(Ⅲ)设集合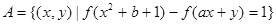 ,
,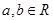 .
.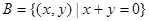 ,若集合
,若集合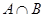 有且仅有一个元素,求证:
有且仅有一个元素,求证: 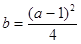 。
。
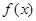 满足
满足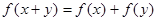 ,且
,且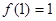 。
。(Ⅰ)判断函数
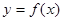 的奇偶性并证明之;
的奇偶性并证明之;(Ⅱ)解关于
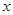 的不等式:
的不等式: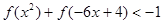 ;
;(Ⅲ)设集合
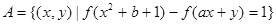 ,
,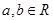 .
.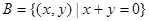 ,若集合
,若集合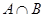 有且仅有一个元素,求证:
有且仅有一个元素,求证: 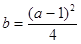 。
。 (Ⅰ)函数为R上的奇函数,(Ⅱ) ,(Ⅲ)见解析
,(Ⅲ)见解析
 ,(Ⅲ)见解析
,(Ⅲ)见解析试题分析:(Ⅰ)抽象函数奇偶性的证明,先令
 ,再令
,再令 可求得出函数为奇函数,(Ⅱ)由(Ⅰ)知
可求得出函数为奇函数,(Ⅱ)由(Ⅰ)知 在
在 上为奇函数,则
上为奇函数,则 利用单调性及
利用单调性及 与-1的关系可解得; (Ⅲ)先对
与-1的关系可解得; (Ⅲ)先对 进行化简,再利用两方程有唯一解
进行化简,再利用两方程有唯一解 求证.
求证.试题解析:(Ⅰ)令
 ,
,

令
 ,
,

 ,
,函数为R上的奇函数. (4分)
(Ⅱ)由(Ⅰ)知


又函数是单调递增函数,

故
 (8分)
(8分)(Ⅲ)



 ,又
,又 有且仅有一个元素,即方程组
有且仅有一个元素,即方程组 有唯一解,
有唯一解,即
 仅有一个实根,
仅有一个实根,  ,即
,即 (13分)
(13分)
练习册系列答案
相关题目
 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 .
.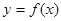 ,
,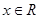 ,
,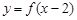 与
与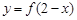 的图象关于直线
的图象关于直线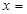 对称;
对称;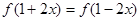 ,则
,则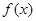 的图象关于直线
的图象关于直线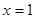 对称;
对称;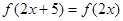 则5是
则5是 ,则
,则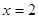 对称;
对称;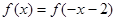 ,则
,则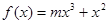 为偶函数,则实数
为偶函数,则实数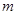 的值为__________.
的值为__________. :
: 的周长和面积同时分为相等的两部分的函数称为圆
的周长和面积同时分为相等的两部分的函数称为圆



 是定义在
是定义在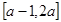 上的偶函数,那么
上的偶函数,那么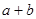 =
= 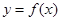 满足条件
满足条件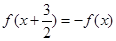 ,且
,且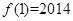 ,则
,则 .
. 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, ,则
,则 = .
= . 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, ,
, =______.
=______.