题目内容
已知椭圆C的中心在原点O,离心率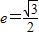 ,右焦点为
,右焦点为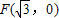 .
.(1)求椭圆C的方程;
(2)设椭圆的上顶点为A,在椭圆C上是否存在点P,使得向量
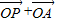 与
与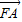 共线?若存在,求直线AP的方程;若不存在,简要说明理由.
共线?若存在,求直线AP的方程;若不存在,简要说明理由.
【答案】分析:(1)设椭圆C的方程为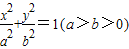 ,由离心率焦点坐标可得及
,由离心率焦点坐标可得及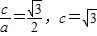 ,再根据a2=b2+c2,联立方程组解出即可;
,再根据a2=b2+c2,联立方程组解出即可;
(2)假设椭圆C上是存在点P(x,y),使得向量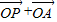 与
与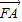 共线,由向量共线及点P在椭圆上得方程组,解出可得点P坐标,进而可求得直线AP方程;
共线,由向量共线及点P在椭圆上得方程组,解出可得点P坐标,进而可求得直线AP方程;
解答:解:(1)设椭圆C的方程为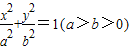 ,
,
∵椭圆C的离心率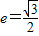 ,右焦点为
,右焦点为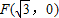 ,∴
,∴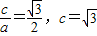 ,
,
∵a2=b2+c2,∴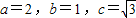 ,
,
故椭圆C的方程为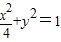 .
.
(2)假设椭圆C上是存在点P(x,y),使得向量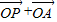 与
与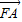 共线,
共线,
∵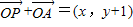 ,
,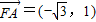 ,∴
,∴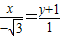 ,即
,即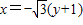 ,(1)
,(1)
又∵点P(x,y)在椭圆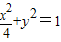 上,∴
上,∴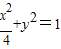 (2),
(2),
由(1)、(2)组成方程组解得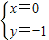 ,或
,或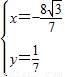 ,
,
∴P(0,-1),或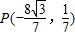 ,
,
当点P的坐标为(0,-1)时,直线AP的方程为x=0,
当点P的坐标为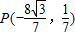 时,直线AP的方程为
时,直线AP的方程为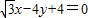 ,
,
故椭圆上存在满足条件的点P,直线AP的方程为x=0或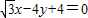 .
.
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及向量共线问题,考查学生分析问题解决问题的能力.
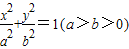 ,由离心率焦点坐标可得及
,由离心率焦点坐标可得及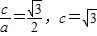 ,再根据a2=b2+c2,联立方程组解出即可;
,再根据a2=b2+c2,联立方程组解出即可;(2)假设椭圆C上是存在点P(x,y),使得向量
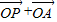 与
与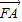 共线,由向量共线及点P在椭圆上得方程组,解出可得点P坐标,进而可求得直线AP方程;
共线,由向量共线及点P在椭圆上得方程组,解出可得点P坐标,进而可求得直线AP方程;解答:解:(1)设椭圆C的方程为
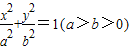 ,
,∵椭圆C的离心率
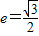 ,右焦点为
,右焦点为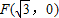 ,∴
,∴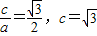 ,
,∵a2=b2+c2,∴
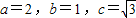 ,
,故椭圆C的方程为
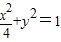 .
. (2)假设椭圆C上是存在点P(x,y),使得向量
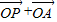 与
与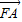 共线,
共线,∵
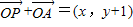 ,
,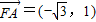 ,∴
,∴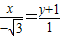 ,即
,即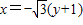 ,(1)
,(1)又∵点P(x,y)在椭圆
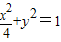 上,∴
上,∴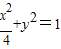 (2),
(2),由(1)、(2)组成方程组解得
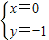 ,或
,或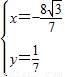 ,
,∴P(0,-1),或
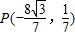 ,
,当点P的坐标为(0,-1)时,直线AP的方程为x=0,
当点P的坐标为
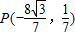 时,直线AP的方程为
时,直线AP的方程为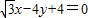 ,
,故椭圆上存在满足条件的点P,直线AP的方程为x=0或
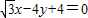 .
.点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及向量共线问题,考查学生分析问题解决问题的能力.

练习册系列答案
相关题目

 。
。