Question

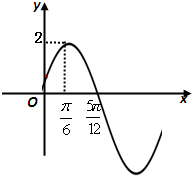已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜

π

2

)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若x∈[0，

π

2

]，求函数f（x）的值域．

Answer 1

分析：（1）由图象求出函数的振幅A，周期，确定ω，利用图象经过(

π

6

，2)确定φ，得到函数的解析式；
（2）根据x∈[0，

π

2

]，2x+

π

6

∈[

π

6

，

7π

6

]，推出-

1

2

≤sin(2x+

π

6

)≤1，可得函数的值域．

解答：解：（1）由图可知A=2，-----1
T=4(

5π

12

-

π

6

)=π，由ω=

2π

T

，得ω=2-----3∴f（x）=2sin（2x+?），又点(

π

6

，2)在图象上，
∴sin(

π

3

+?)=1，∴?=

π

6

+2kπ，k∈z，又|?|＜

π

2

，∴?=

π

6

-------5
∴f(x)=2sin(2x+

π

6

)----------6
（2）∵x∈[0，

π

2

]，∴2x+

π

6

∈[

π

6

，

7π

6

]，-----8′∴-

1

2

≤sin(2x+

π

6

)≤1-----11′，
∴函数f（x）的值域为[-1，2]．-----------12

点评：本题是基础题，考查三角函数的化简求值，函数的解析式的求法，考查计算能力，常考题型．