题目内容
某厂生产甲、乙两种产品,计划产量分别为45个、50个,所用原料为A、B两种规格的金属板,每张面积分别为2m2、3m2,用A种金属板可造甲产品3个,乙产品5个,用B种金属板可造甲、乙产品各6个,则能完成计划产量时总用料面积最少为 m2.
【答案】分析:设A、B两种金属板各取x张、y张,用料面积z,写出约束条件、目标函数,作出可行域,即可求得结论.
解答:解:设A、B两种金属板各取x张、y张,用料面积z,则约束条件为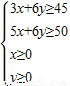 ,目标函数z=2x+3y.
,目标函数z=2x+3y.
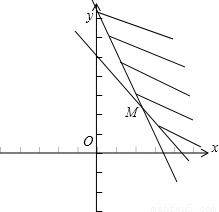
作出以上不等式组所表示的平面区域,即可行域,如图所示.
z=2x+3y变为y=- x+
x+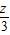 ,得斜率为-
,得斜率为- ,在y轴上的截距为
,在y轴上的截距为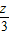 ,且随z变化的一组平行线.
,且随z变化的一组平行线.
当直线z=2x+3y过可行域上的点M时,截距最小,z最小.
解方程组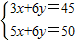 得M点的坐标为(2.5,6.25),
得M点的坐标为(2.5,6.25),
又由x、y都为正整数,分析可得当x=3、y=6时,z取得最小值.
此时zmin=2×3+3×6=24(m2).
故答案为:24.
点评:本题考查利用线性规划知识,解决最值问题,确定约束条件、目标函数是关键.
解答:解:设A、B两种金属板各取x张、y张,用料面积z,则约束条件为
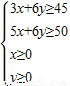 ,目标函数z=2x+3y.
,目标函数z=2x+3y.作出以上不等式组所表示的平面区域,即可行域,如图所示.

z=2x+3y变为y=-
 x+
x+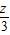 ,得斜率为-
,得斜率为- ,在y轴上的截距为
,在y轴上的截距为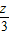 ,且随z变化的一组平行线.
,且随z变化的一组平行线.当直线z=2x+3y过可行域上的点M时,截距最小,z最小.
解方程组
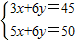 得M点的坐标为(2.5,6.25),
得M点的坐标为(2.5,6.25),又由x、y都为正整数,分析可得当x=3、y=6时,z取得最小值.
此时zmin=2×3+3×6=24(m2).
故答案为:24.
点评:本题考查利用线性规划知识,解决最值问题,确定约束条件、目标函数是关键.

练习册系列答案
相关题目