题目内容
设各项均为正数的数列{an}满足a1=2,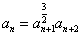 (n∈N*),
(n∈N*),
(Ⅰ)若a2=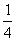 ,求a3,a4,并猜想a2008的值(不需证明);
,求a3,a4,并猜想a2008的值(不需证明);
(Ⅱ)若2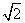 ≤a1a2…an<4对n≥2恒成立,求a2的值。
≤a1a2…an<4对n≥2恒成立,求a2的值。
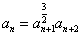 (n∈N*),
(n∈N*),(Ⅰ)若a2=
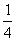 ,求a3,a4,并猜想a2008的值(不需证明);
,求a3,a4,并猜想a2008的值(不需证明);(Ⅱ)若2
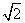 ≤a1a2…an<4对n≥2恒成立,求a2的值。
≤a1a2…an<4对n≥2恒成立,求a2的值。 解:(Ⅰ)因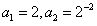 ,
,
故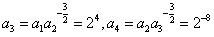 ,
,
由此有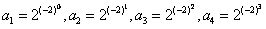 ,
,
故猜想|an|的通项为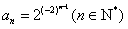 ,
,
从而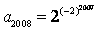 ;
;
(Ⅱ)令xn=log2an,则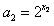 ,故只需求x2的值。
,故只需求x2的值。
设Sn表示xn的前n项和,则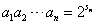 ,
,
由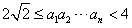 得
得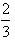 ≤Sn=x1+x2+…+xn<2(n≥2),
≤Sn=x1+x2+…+xn<2(n≥2),
因上式对n=2成立,可得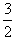 ≤x1+x2,
≤x1+x2,
又由a1=2,得x1=1,故x2≥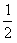 ,
,
由于a1=2,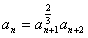 (n∈N*),得
(n∈N*),得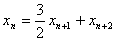 (n∈N*),
(n∈N*),
即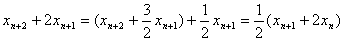 ,
,
因此数列{xn+1+2xn}是首项为x2+2,公比为 的等比数列,
的等比数列,
故xn+1+2xn=(x2+2)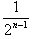 (n∈N*),
(n∈N*),
将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+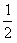 +…+
+…+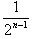 )=(x2+2)(2-
)=(x2+2)(2-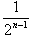 )(n≥2),
)(n≥2),
因Sn<2,Sn+1<2(n≥2)且x1=1,
故(x2+2)(2-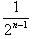 )<5(n≥2),
)<5(n≥2),
因此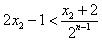 (n≥2),
(n≥2),
下证x2≤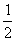 ,
,
若不然,假设x2>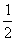 ,
,
则由上式知,不等式2n-1<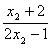 对n≥2恒成立,但这是不可能的,
对n≥2恒成立,但这是不可能的,
因此x2≤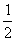 ;
;
又x2≥ ,
,
故x2=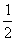 ,
,
所以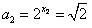 。
。
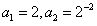 ,
,故
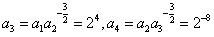 ,
,由此有
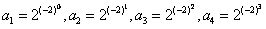 ,
,故猜想|an|的通项为
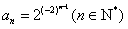 ,
,从而
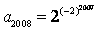 ;
;(Ⅱ)令xn=log2an,则
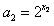 ,故只需求x2的值。
,故只需求x2的值。设Sn表示xn的前n项和,则
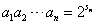 ,
,由
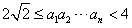 得
得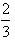 ≤Sn=x1+x2+…+xn<2(n≥2),
≤Sn=x1+x2+…+xn<2(n≥2),因上式对n=2成立,可得
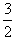 ≤x1+x2,
≤x1+x2,又由a1=2,得x1=1,故x2≥
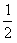 ,
,由于a1=2,
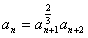 (n∈N*),得
(n∈N*),得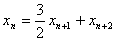 (n∈N*),
(n∈N*),即
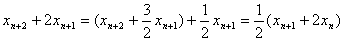 ,
,因此数列{xn+1+2xn}是首项为x2+2,公比为
 的等比数列,
的等比数列,故xn+1+2xn=(x2+2)
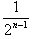 (n∈N*),
(n∈N*),将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+
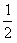 +…+
+…+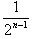 )=(x2+2)(2-
)=(x2+2)(2-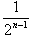 )(n≥2),
)(n≥2),因Sn<2,Sn+1<2(n≥2)且x1=1,
故(x2+2)(2-
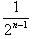 )<5(n≥2),
)<5(n≥2),因此
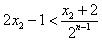 (n≥2),
(n≥2),下证x2≤
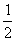 ,
,若不然,假设x2>
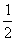 ,
,则由上式知,不等式2n-1<
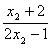 对n≥2恒成立,但这是不可能的,
对n≥2恒成立,但这是不可能的,因此x2≤
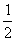 ;
;又x2≥
 ,
,故x2=
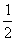 ,
,所以
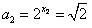 。
。 
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目