题目内容
20.如图，在直四棱柱ABCD－A1B1C1D1中，已知DC=DD1=2AD=2AB，AD⊥DC，AB∥DC.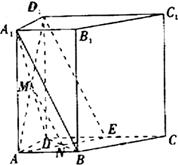
(Ⅰ)求证：D1C⊥AC1;
(Ⅱ)设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由.
解：(Ⅰ)证明：在直四棱柱ABCD－A1B1C1D1中.
连结C1D，
∵DC=DD1.
∵四边形DCC1D1是正方形，
∴DC1⊥D1C，
又AD⊥DC，AD⊥DD1，DC∩DD1=D，
∴AD⊥平面DCC1D1，
D1C
平面DCC1D1，
∴AD⊥D1C，
∵AD，DC1
平面ADC1，
且AD∩DC1=D
∴D1C⊥平面ADC1，
又AC1
平面ADC1，
∴D1C⊥AC1.
(Ⅱ)连结AD1，连结AE，
设AD1∩A1D=M，
BD∩AE=N，连结MN.
∵平面AD1E∩平面A1BD=MN，
要使D1E∥平面A1BD，
须使MN∥D1E.
又M是AD1的中点，
∴N是AE的中点.
又易知△ABN≌△EDN.
∴AB=DE.
即E是DC的中点.
综上所述，当E是DC的中点对，可使D1E∥平面A1BD.
练习册系列答案
相关题目
18、如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E，E1分别是棱AD，AA1的中点，F为AB的中点．证明：
18、如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E，E1分别是棱AD，AA1的中点．
15、如图，在直四棱柱ABCD-A1B1C1D1中，A1C1⊥B1D1，E，F分别是AB，BC的中点．
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E，E1，F分别是棱AD，AA1，AB的中点．
（2010•抚州模拟）如图，在直四棱柱ABCD-A1B1C1D1中，AB=BC，∠ABC=60°，BB1=BC=2，M为BC中点，点N在CC1上．