题目内容
设点F( ,0)(p为正常数),点M在x轴的负半轴上,点P在y轴上,且
,0)(p为正常数),点M在x轴的负半轴上,点P在y轴上,且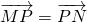 ,
,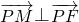 .
.
(Ⅰ)当点P在y轴上运动时,求点N的轨迹C的方程;
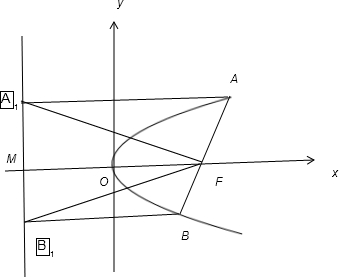
(Ⅱ)直线l过点F且与曲线C相交于不同两点A,B,分别过点A,B作直线l1:x=- 的垂线,对应的垂足分别为A1,B1,求
的垂线,对应的垂足分别为A1,B1,求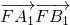 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,记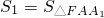 ,
,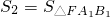 ,
,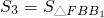 ,λ=
,λ=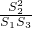 ,求λ的值.
,求λ的值.
解:(1)设N(x,y),M(a,0),(a>0),P(0,b)
由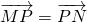 可得,x=-a,y=2b①
可得,x=-a,y=2b①
由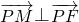 可得
可得 ②
②
①②联立可得y2=2px(p>0)
(2)由抛物线的定义可得AF=AA1,BF=BB1,AA1∥MF∥BB1
∴∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
∴∠A1FB1=∠B1FM+∠MFA1=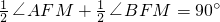
即FA1⊥FB1∴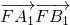 =0
=0
(3)设直线AB的方程为:x=ky+ A(x1,y1) B(x2,y2)
A(x1,y1) B(x2,y2)
联立方程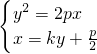 整理可得y2-2pky-p2=0
整理可得y2-2pky-p2=0
则y1+y2=2pk,y1y2=-p2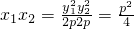 x1+x2=k(y1+y2)+p=2pk2+p
x1+x2=k(y1+y2)+p=2pk2+p
λ=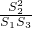 =
=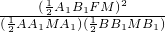 =
=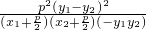 =
=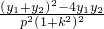
=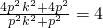
分析:(1)设N(x,y),M(a,0),(a>0),P(0,b),由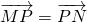 可得,x=-a,y=2b,由
可得,x=-a,y=2b,由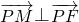 可得
可得 ,从而可求x,y满足的方程
,从而可求x,y满足的方程
(2)由抛物线的定义可得AF=AA1,BF=BB1,AA1∥MF∥BB1
从而有∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
则有∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
∠A1FB1=∠B1FM+∠MFA1=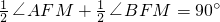
(3)设直线AB的方程为:x=ky+ A(x1,y1) B(x2,y2)
A(x1,y1) B(x2,y2)
联立方程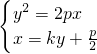 整理可得y2-2pky-p2=0
整理可得y2-2pky-p2=0
则y1+y2=2pk,y1y2=-p2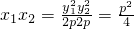 x1+x2=k(y1+y2)+p=2pk2+p
x1+x2=k(y1+y2)+p=2pk2+p
λ=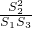 =
=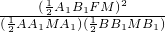 代入整理可求
代入整理可求
点评:本题以平面向量向量的基本运算为载体,重点考查了抛物线的性质的应用,直线与抛物线的位置关系等知识的综合运用,解决本题(2)的关键是要熟练掌握抛物线的定义发现AF=AA1,BF=BB1,解决(3)时要注意设直线方程时为了避免讨论斜率k的值是否存在,故可设直线AB的方程为:x=ky+
由
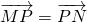 可得,x=-a,y=2b①
可得,x=-a,y=2b①由
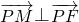 可得
可得 ②
②①②联立可得y2=2px(p>0)
(2)由抛物线的定义可得AF=AA1,BF=BB1,AA1∥MF∥BB1
∴∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
∴∠A1FB1=∠B1FM+∠MFA1=
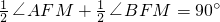
即FA1⊥FB1∴
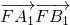 =0
=0(3)设直线AB的方程为:x=ky+
 A(x1,y1) B(x2,y2)
A(x1,y1) B(x2,y2)联立方程
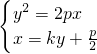 整理可得y2-2pky-p2=0
整理可得y2-2pky-p2=0则y1+y2=2pk,y1y2=-p2
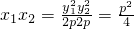 x1+x2=k(y1+y2)+p=2pk2+p
x1+x2=k(y1+y2)+p=2pk2+pλ=
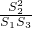 =
=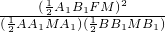 =
=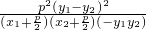 =
=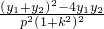
=
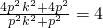

分析:(1)设N(x,y),M(a,0),(a>0),P(0,b),由
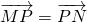 可得,x=-a,y=2b,由
可得,x=-a,y=2b,由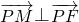 可得
可得 ,从而可求x,y满足的方程
,从而可求x,y满足的方程(2)由抛物线的定义可得AF=AA1,BF=BB1,AA1∥MF∥BB1
从而有∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
则有∠AFA1=∠AA1F=∠MFA1,∠BFB1=∠BB1F=∠MFB1
∠A1FB1=∠B1FM+∠MFA1=
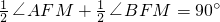
(3)设直线AB的方程为:x=ky+
 A(x1,y1) B(x2,y2)
A(x1,y1) B(x2,y2)联立方程
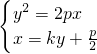 整理可得y2-2pky-p2=0
整理可得y2-2pky-p2=0则y1+y2=2pk,y1y2=-p2
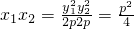 x1+x2=k(y1+y2)+p=2pk2+p
x1+x2=k(y1+y2)+p=2pk2+pλ=
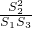 =
=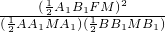 代入整理可求
代入整理可求点评:本题以平面向量向量的基本运算为载体,重点考查了抛物线的性质的应用,直线与抛物线的位置关系等知识的综合运用,解决本题(2)的关键是要熟练掌握抛物线的定义发现AF=AA1,BF=BB1,解决(3)时要注意设直线方程时为了避免讨论斜率k的值是否存在,故可设直线AB的方程为:x=ky+


练习册系列答案
相关题目
 已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为
已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为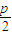 ,0)(p为正常数),点M在x轴的负半轴上,点P在y轴上,且
,0)(p为正常数),点M在x轴的负半轴上,点P在y轴上,且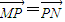 ,
,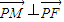 .
.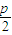 的垂线,对应的垂足分别为A1,B1,求
的垂线,对应的垂足分别为A1,B1,求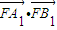 的值;
的值;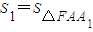 ,
,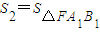 ,
,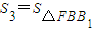 ,λ=
,λ=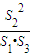 ,求λ的值.
,求λ的值.