Question

设数列{a_n}满足a₁=2,a_n+1=a_n+(n=1,2,3，…).

(1)证明：a_n＞对一切正整数n成立；

(2)令b_n=(n=1,2,3,…)，判断b_n与b_n+1的大小，并说明理由.

Answer 1

(1)证明：当n=1时，a₁=2＞,不等式成立.

假设n=k时，a_k＞成立.

当n=k+1时，a_k+1²=a_k²++2＞2k+3+＞2(k+1)+1,

∴n=k+1时，a_k+1＞成立.

综上由数学归纳法可知，a_n＞对一切正整数成立.

(2)解析：

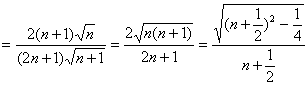＜1.故b_n+1＜b_n.