题目内容
已知函数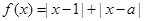 .
.
(1)若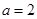 ,解不等式
,解不等式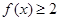 ;
;
(2)若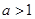 ,
,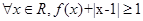 ,求实数
,求实数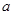 的取值范围.
的取值范围.
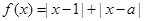 .
.(1)若
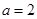 ,解不等式
,解不等式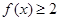 ;
;(2)若
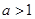 ,
,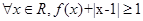 ,求实数
,求实数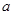 的取值范围.
的取值范围.(1) 或
或 ;(2)
;(2) .
.
 或
或 ;(2)
;(2) .
.试题分析:本题考查绝对值不等式的解法和不等式的恒成立问题,考查学生的分类讨论思想和转化能力.第一问,利用零点分段法进行求解;第二问,利用函数的单调性求出最小值证明恒成立问题.
试题解析:(1)当
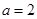 时,
时, ,而
,而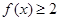 ,
,解得
 或
或 . 5分
. 5分(2)令
 ,则
,则 ,
,所以当
 时,
时, 有最小值
有最小值 ,
,只需
 ,解得
,解得 ,所以实数
,所以实数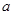 的取值范围为
的取值范围为 . 10分
. 10分
练习册系列答案
相关题目
 的最大值为
的最大值为 .
. ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ; 的所有实数a.
的所有实数a.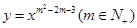 的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-
的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-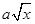 在(0,1)上为减函数.
在(0,1)上为减函数. ,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足
,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足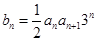 ,
, ,求数列{an}的通项公式an和sn.
,求数列{an}的通项公式an和sn.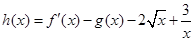 ,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.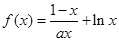
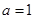 时,求
时,求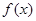 在
在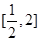 上的最小值;
上的最小值;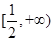 上为增函数,求正实数
上为增函数,求正实数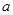 的取值范围;
的取值范围;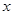 的方程
的方程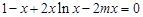 在区间
在区间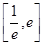 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数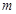 的取值范围.
的取值范围.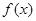 的定义域为D,若对于任意
的定义域为D,若对于任意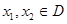 ,当
,当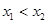 时都有
时都有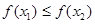 ,则称函数
,则称函数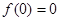 ;②
;②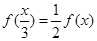 ;③
;③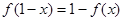 ,则
,则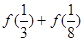 等于( )
等于( )


 满足:当
满足:当 时,
时, ,则在R上,函数
,则在R上,函数 +2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
+2bx+c,若a+b+c=0,且F(0)>0,F(1)>0. <—1.
<—1. ,求
,求 =
=  ,则
,则 ( )
( )