题目内容
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 当且仅当“
当且仅当“ ”或“
”或“ ”.按上述定义的关系“
”.按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若 ;
;
②若 ,则
,则 ;
;
③若 ,则对于任意
,则对于任意 ;
;
④对于任意向量 .
.
其中真命题的序号为__________.
①②③
解析试题分析:①因为 由定义,
由定义, ,所以
,所以
故①为真命题;
②设 由
由 得:
得: ,或
,或
由 得
得 ,或
,或 ,以下分四种情况讨论:
,以下分四种情况讨论:
第一:若 ,
, 则
则 ,所以
,所以
第二:若 ,
, 则
则 ,所以
,所以
第三:若 ,
, 则
则 ,所以
,所以
第四:若 ,
, 则
则 ,所以,
,所以, 且
且 所以
所以
所以②是真命题
③设
 ,则
,则
由 得:“
得:“ ”或“
”或“ ”所以
”所以 或“
或“ 且
且 ”
”
所以是真命题.
④设 ,显然满足
,显然满足
 ,但
,但 =
= ,
,
所以 ,所以命题是假命题.
,所以命题是假命题.
综上答案应填①②③.
考点:1、新定义;2、不等式的性质;3、向量的概念与运算.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知向量a  ,b
,b ,向量c满足(c
,向量c满足(c b)
b) a,(c
a,(c a)//b,则c
a)//b,则c ( )
( )
A. | B. | C. | D. 高@考3资%源**网 高@考3资%源**网 |
在实轴上有两点 ,则实轴上的向量
,则实轴上的向量 的数量是:( )
的数量是:( )
A. | B. | C. | D. |
 =λ
=λ 中,已知
中,已知 ,
,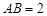 ,
, ,
, ,
, ,则
,则 .
.
 ,则点B的坐标为.
,则点B的坐标为. ,
, ,
, ,若
,若 三点共线,则实数
三点共线,则实数 的值为 _ .
的值为 _ .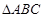 中,若
中,若 则
则
 为平面上以
为平面上以 为顶点的三角形区域(包括边界)上一动点,
为顶点的三角形区域(包括边界)上一动点, 为原点,且
为原点,且 ,则
,则 的取值范围为 .
的取值范围为 .