若直线和⊙O∶相离,则过点的直线与椭圆的交点个数为A. 至多一个 B. 2个 C. 1个 D. 0个题目和参考答案——青夏教育精英家教网—

题目内容

若直线和⊙O∶相离,则过点的直线与椭圆的交点个数为（）

A. 至多一个 B. 2个 C. 1个 D. 0个

【解析】

试题分析：由题可知，直线和⊙O∶相离，因此有，而椭圆的短半轴为2，因此经过点的直线与椭圆的交点个数为2个；

考点：直线与圆锥曲线的位置关系

考点分析： 考点1：椭圆的标准方程 考点2：椭圆的几何性质 试题属性

练习册系列答案

成功训练计划系列答案

相关题目

函数的单调递减区间为．

（本题满分6分）某校高二年级的一次数学考试中，为了分析学生的得分情况，随机抽取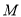名同学的成绩，数据的分组统计表如下：

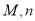（1）求出表中的值；

（2）为了了解某些同学在数学学习中存在的问题，现从样本中分数在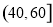中的6位同学中任意抽取2人进行调查，求分数在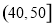和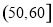中各有一人的概率．

（本小题满分12分）已知是抛物线上一点，经过点的直线与抛物线交于两点（不同于点），直线分别交直线于点.

（1）求抛物线方程及其焦点坐标；

（2）已知为原点，求证：为定值.

在内任取一个实数，设，则函数的图像与轴有公共点的概率等于。

一个棱锥的三视图如图所示，则这个棱锥的体积是（）

A．6 B．12 C．24 D．36

（本小题满分14分）已知

（1）求的最小正周期及；

（2）求的单调增区间；

（3）当时，求的值域．

已知函数．

若时函数有三个互不相同的零点，求实数的取值范围；

若对任意的，不等式对任意恒成立，求实数的取值范围．

空间直角坐标系中,点关于平面对称的点的坐标为（）

A． B． C． D．

试题分类