题目内容
已知函数 ,对任意实数
,对任意实数 都有
都有 成立,若当
成立,若当 时,
时, 恒成立,则
恒成立,则 的取值范围是
的取值范围是
A.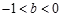 | B. 或 或  | C. | D.不能确定 |
B
解析试题分析:因为函数对任意实数 都有
都有 成立,所以函数关于
成立,所以函数关于 对称,又因为二次函数
对称,又因为二次函数 的对称轴为
的对称轴为 ,可以得到
,可以得到 ,又函数在区间
,又函数在区间 上单调递增,所以若
上单调递增,所以若 时,
时, 恒成立
恒成立
 ,对
,对
 时,
时, 恒成立,即
恒成立,即 ,进而求得
,进而求得 或
或 
考点:本题考查了二次函数的对称性以及区间上函数单调性与对称轴以及二次函数图像开口方向之间的关系,同时又将恒成立问题转化成最值问题求解的思想嵌入此题,实属不易。
点评:本题难度有所拔高,把单调性、对称性、恒成立问题、最值问题柔和在一起组成此题,虽然难度上有所拔高,对学生的逻辑推理以及分析问题的能力的要求都有所提高,但本题确实是一道一见的好题。

练习册系列答案
相关题目
若函数 与
与 的定义域均为R,则( )
的定义域均为R,则( )
| A.f(x)与g(x)均为偶函数 | B.f(x)为偶函数,g(x)为奇函数 |
| C.f(x)与g(x)均为奇函数 | D.f(x)为奇函数,g(x)为偶函数 |
下列函数中与函数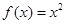 相等的是( )
相等的是( )
A. | B. |
C. | D.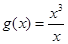 |
方程 的解所在的区间为
的解所在的区间为
A. | B. | C. | D. |
函数 的单减区间是( )
的单减区间是( )
A. | B. | C. | D. |
已知函数 在
在 上是增函数,则
上是增函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
下列函数中是奇函数的是( )
A. | B. | C. | D. |
设 ,用二分法求方程
,用二分法求方程 在
在 内近似解的过程中得
内近似解的过程中得 ,则方程的根落在区间( )
,则方程的根落在区间( )
A. | B. | C. | D.不能确定 |
 的图象大致是( )
的图象大致是( )