题目内容
已知方程为x2+y2-3x+ay-3=0表示圆,则a的范围________.
a∈R
分析:将方程配方成标准形式,可得它表示以C( ,-
,- )为圆心,半径r=
)为圆心,半径r= 的圆,不论a为何实数,方程总能表示一个圆.由此可得实数a的范取值围.
的圆,不论a为何实数,方程总能表示一个圆.由此可得实数a的范取值围.
解答:方程x2+y2-3x+ay-3=0进行配方,得(x- )2+(y+
)2+(y+ )2=
)2=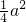 +
+ ,
,
∴已知方程x2+y2-3x+ay-3=0表示以C( ,-
,- )为圆心,半径r=
)为圆心,半径r= >0
>0
不管a为何实数,总有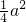 +
+ >0,方程总能表示圆
>0,方程总能表示圆
∴实数a的范取值围是R
故答案为:a∈R
点评:本题给出二次曲线方程表示一个圆,求参数a的取值范围,着重考查了圆的方程的几种形式及其相互转化的知识,属于基础题.
分析:将方程配方成标准形式,可得它表示以C(
 ,-
,- )为圆心,半径r=
)为圆心,半径r= 的圆,不论a为何实数,方程总能表示一个圆.由此可得实数a的范取值围.
的圆,不论a为何实数,方程总能表示一个圆.由此可得实数a的范取值围.解答:方程x2+y2-3x+ay-3=0进行配方,得(x-
 )2+(y+
)2+(y+ )2=
)2=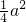 +
+ ,
,∴已知方程x2+y2-3x+ay-3=0表示以C(
 ,-
,- )为圆心,半径r=
)为圆心,半径r= >0
>0不管a为何实数,总有
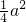 +
+ >0,方程总能表示圆
>0,方程总能表示圆∴实数a的范取值围是R
故答案为:a∈R
点评:本题给出二次曲线方程表示一个圆,求参数a的取值范围,着重考查了圆的方程的几种形式及其相互转化的知识,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目