题目内容
若非零向量 、
、 满足|
满足| 一
一 |=|
|=| |,则( )
|,则( )①向量
 、
、 的夹角恒为锐角 ②2|
的夹角恒为锐角 ②2| |2>
|2> .
. ③|2
③|2 |>|
|>| 一2
一2 |④|2
|④|2 |<|2
|<|2 一
一 |
|A.1个
B.2个
C.3个
D.4个
【答案】分析:利用向量的平方等于向量模的平方,将已知等式平方,得到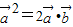 ,利用两个向量都是非零向量得到两个向量的数量积大于0判断出①对,据已知条件得不到数量积与
,利用两个向量都是非零向量得到两个向量的数量积大于0判断出①对,据已知条件得不到数量积与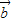 的模的关系判断出②错,将③平方判断出③对;将④平方,由于已知条件得不到数量积与
的模的关系判断出②错,将③平方判断出③对;将④平方,由于已知条件得不到数量积与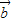 的模的关系判断出④错.
的模的关系判断出④错.
解答:解:∵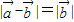
∴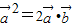
对于①,∵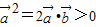 ,∴两个向量的夹角为锐角,故①对
,∴两个向量的夹角为锐角,故①对
对于②,非零向量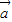 、
、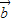 满足|
满足|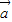 一
一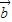 |=|
|=|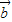 |,2|
|,2|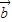 |2>
|2>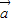 .
.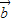 ,故②正确.
,故②正确.
对于③即为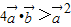 ,∵
,∵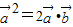 ,∴③对
,∴③对
对于④,即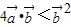 不确定,故④错
不确定,故④错
故选C.
点评:解决向量模的有关问题,一般利用向量模的平方等于向量的平方,将模的问题转化为向量的问题来解决.
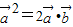 ,利用两个向量都是非零向量得到两个向量的数量积大于0判断出①对,据已知条件得不到数量积与
,利用两个向量都是非零向量得到两个向量的数量积大于0判断出①对,据已知条件得不到数量积与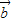 的模的关系判断出②错,将③平方判断出③对;将④平方,由于已知条件得不到数量积与
的模的关系判断出②错,将③平方判断出③对;将④平方,由于已知条件得不到数量积与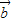 的模的关系判断出④错.
的模的关系判断出④错.解答:解:∵
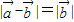
∴
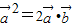
对于①,∵
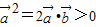 ,∴两个向量的夹角为锐角,故①对
,∴两个向量的夹角为锐角,故①对对于②,非零向量
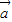 、
、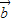 满足|
满足|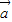 一
一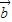 |=|
|=|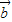 |,2|
|,2|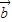 |2>
|2>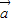 .
.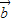 ,故②正确.
,故②正确.对于③即为
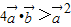 ,∵
,∵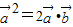 ,∴③对
,∴③对对于④,即
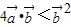 不确定,故④错
不确定,故④错故选C.
点评:解决向量模的有关问题,一般利用向量模的平方等于向量的平方,将模的问题转化为向量的问题来解决.

练习册系列答案
相关题目
若非零 向量
向量 、
、 满足|
满足| 一
一 |=|
|=| |,则下面说法恒成立的有
|,则下面说法恒成立的有
①向量 、
、 的夹角恒为锐角 ②
的夹角恒为锐角 ②  >
>
③|2 |>|
|>| 一2
一2 | ④|2
| ④|2 |<|2
|<|2 一
一 |
|
A.1个 | B.2 个 个 | C.3个 | D.4个 |
 、
、 满足|
满足| >
>