题目内容
(本小题满分12分)
(Ⅰ)一动圆与圆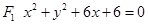 相外切,与圆
相外切,与圆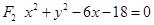 相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。
相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。
(Ⅱ)过点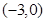 作一直线
作一直线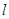 与曲线E交与A,B两点,若
与曲线E交与A,B两点,若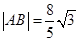 ,求此时直线
,求此时直线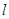 的方程。
的方程。
(Ⅰ)一动圆与圆
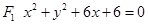 相外切,与圆
相外切,与圆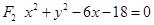 相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。
相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。(Ⅱ)过点
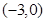 作一直线
作一直线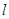 与曲线E交与A,B两点,若
与曲线E交与A,B两点,若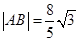 ,求此时直线
,求此时直线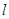 的方程。
的方程。解:(1)设动圆圆心的坐标为
 ,半径为r
,半径为r又内切和外切的几何意义



所以所求曲线轨迹为椭圆,

方程为:

⑵设直线方程为
 直线与椭圆交与A
直线与椭圆交与A , B
, B 
联立方程组
 把直线方程代入椭圆方程化简整理得
把直线方程代入椭圆方程化简整理得 ①
①

又弦长公式
 ,代入解的
,代入解的
所以直线方程为

略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
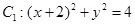 及点
及点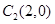 ,在圆
,在圆 上任取一点
上任取一点 ,连接
,连接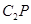 ,做线段
,做线段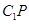 于点
于点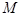 .
.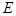 的方程;
的方程;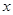 轴交于
轴交于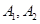 两点,在轨迹
两点,在轨迹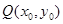
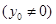 ,直线
,直线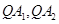 分别交
分别交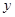 轴于
轴于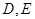 两点,求证:以线段
两点,求证:以线段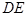 为直径的圆
为直径的圆 过两个定点,并求出定点坐标.
过两个定点,并求出定点坐标. :
: 和圆
和圆 :
: 的位置关系( )
的位置关系( )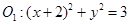 外切,与圆
外切,与圆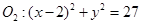 内切.
内切.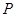 ,使直线
,使直线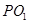 与
与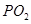 的斜率
的斜率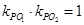 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)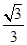 ,
,
 与圆
与圆 外切,与直线
外切,与直线 相切,则
相切,则 与圆
与圆 相交,则实数
相交,则实数 的取值范围为 ▲
的取值范围为 ▲ ,
, ,则
,则 和
和 的位置关系是
的位置关系是 和
和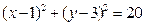 相交于
相交于 两点,则直线
两点,则直线 的方程是 。
的方程是 。