题目内容
利用性质解题
（1）已知y=f（x）是（-3，3）上的减函数，解不等式f（x+3）＞f（2-x）；
（2）定义在（-1，1）上的奇函数f（x）是减函数，且满足条件f（1-a）+f（1-2a）＜0，求a的取值范围．
（1）已知y=f（x）是（-3，3）上的减函数，解不等式f（x+3）＞f（2-x）；
（2）定义在（-1，1）上的奇函数f（x）是减函数，且满足条件f（1-a）+f（1-2a）＜0，求a的取值范围．
分析：（1）根据y=f（x）是（-3，3）上的减函数，解不等式f（x+3）＞f（2-x）即可；
（2）根据汉奇偶性和单调性之间的关系解不等式即可．
（2）根据汉奇偶性和单调性之间的关系解不等式即可．
解答：解：（1）∵y=f（x）是（-3，3）上的减函数，
∴不等式f（x+3）＞f（2-x）等价为：
，
即
，∴-1＜x＜-
，
即不等式的解集为（-1，-
）．
（2）∵f（x）是在（-1，1）上的奇函数，
∴f（1-a）+f（1-2a）＜0，等价为f（1-a）＜-f（1-2a）=f（2a-1），
∵f（x）是减函数，
∴
，
即
，
∴0＜a＜
．
即a的取值范围0＜a＜
．
∴不等式f（x+3）＞f（2-x）等价为：
|
即
|
| 1 |
| 2 |
即不等式的解集为（-1，-
| 1 |
| 2 |
（2）∵f（x）是在（-1，1）上的奇函数，
∴f（1-a）+f（1-2a）＜0，等价为f（1-a）＜-f（1-2a）=f（2a-1），
∵f（x）是减函数，
∴
|
即
|
∴0＜a＜
| 2 |
| 3 |
即a的取值范围0＜a＜
| 2 |
| 3 |
点评：本题主要考查函数奇偶性和单调性之间的应用，综合考查函数性质的应用．
练习册系列答案
相关题目
上存在两个不同点关于直线y=x对称，求出其坐标；若曲线
（p≠0）上存在两个不同点关于直线y=x对称，求实数p的范围；
及
加以研究．当0＜a＜1时，就函数y=ax与y=logax的图象的交点情况提出你的问题，并加以解决．（说明：①函数f（x）=xlnx有如下性质：在区间
上单调递减，在区间
上单调递增．解题过程中可以利用；②将根据提出和解决问题的不同层次区别给分．）
（p≠0）上存在两个不同点关于直线y=x对称，求实数p的取值范围；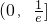
上单调递减，在区间
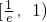上单调递增．解题过程中可以利用；②将根据提出和解决问题的不同层次区别给分．）