题目内容
20.已知抛物线y=-x2+4x-3及其上两点A(0,-3),B(3,0),(1)分别求抛物线在A,B两点处的切线方程;
(2)求由抛物线及其在A,B两点处的切线共同围成的图形的面积.
分析 (1)求导数,确定抛物线在A,B两点处的切线的斜率,即可求抛物线在A,B两点处的切线方程;
(2)由$\left\{\begin{array}{l}y=4x-3\\ y=-2x+6\end{array}\right.$得$x=\frac{3}{2}$,利用定积分求由抛物线及其在A,B两点处的切线共同围成的图形的面积.
解答 解:(1)因为y'=-2x+4,
所以抛物线在A,B两点处的切线的斜率分别为4和-2,
其切线方程分别为:y=4x-3和y=-2x+6
(2)由$\left\{\begin{array}{l}y=4x-3\\ y=-2x+6\end{array}\right.$得$x=\frac{3}{2}$
故$S=\int_0^{\frac{3}{2}}{({4x-3+{x^2}-4x+3})}dx+\int_{\frac{3}{2}}^3{({-2x+6+{x^2}-4x+3})}dx$
=$\frac{1}{3}{x^3}\left|\begin{array}{l}\frac{3}{2}\\ 0\end{array}\right.+$$({\frac{1}{3}{x^3}-3{x^2}+9x})\left|\begin{array}{l}3\\ \frac{3}{2}\end{array}\right.$=$\frac{9}{4}$.
点评 本题考查导数的几何意义,考查定积分知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.过抛物线x2=2py(p>0)焦点F作倾斜角为30°的直线,与拋物线分别交于A,B两点(点A在y轴左侧),则$\frac{|AF|}{|FB|}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
15.过点P(1,1)的直线被圆x2+y2=4截得的弦取得最小值,则该直线的方程为( )
| A. | x+y-2=0 | B. | y-1=0 | C. | x-y=0 | D. | x+3y-4=0 |
5.设f′(x)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
| A. | 不存在 | B. | 与x轴平行或重合 | C. | 与x轴垂直 | D. | 与x轴相交不垂直 |
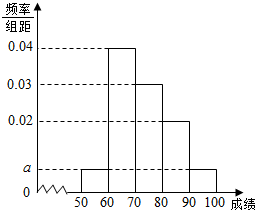 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].