题目内容
已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=ax(a>1),(1)求函数f(x)的解析式;
(2)若不等式f(x)≤4的解集为[-2,2],求a的值.
【答案】分析:(1)当x<0时,-x>0,由已知表达式求出f(-x),然后根据奇偶性求出f(x);
(2)由a>1得,f(x)≤4等价于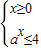 或
或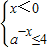 ,再根据不等式的解集可求出a值;
,再根据不等式的解集可求出a值;
解答:(1)当x<0时,-x>0,f(-x)=a-x,
又f(x)为偶函数,所以f(x)=f(-x)=a-x,
所以f(x)=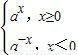 ;
;
(2)因为a>1,所以f(x)≤4等价于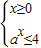 或
或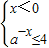 ,
,
所以0≤x≤loga4或-loga4≤x<0,
由条件知loga4=2,所以a=2.
点评:本题考查函数的奇偶性及对数不等式的解法,考查学生的运算能力、分析问题解决问题的能力.
(2)由a>1得,f(x)≤4等价于
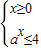 或
或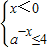 ,再根据不等式的解集可求出a值;
,再根据不等式的解集可求出a值;解答:(1)当x<0时,-x>0,f(-x)=a-x,
又f(x)为偶函数,所以f(x)=f(-x)=a-x,
所以f(x)=
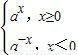 ;
;(2)因为a>1,所以f(x)≤4等价于
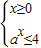 或
或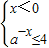 ,
,所以0≤x≤loga4或-loga4≤x<0,
由条件知loga4=2,所以a=2.
点评:本题考查函数的奇偶性及对数不等式的解法,考查学生的运算能力、分析问题解决问题的能力.

练习册系列答案
相关题目