题目内容
【题目】已知直线l: 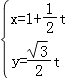 (t为参数),曲线C1:
(t为参数),曲线C1: ![]() (θ为参数).
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 ![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 ![]() 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
【答案】解:(I)l的普通方程为y= ![]() (x﹣1),C1的普通方程为x2+y2=1,
(x﹣1),C1的普通方程为x2+y2=1,
联立方程组 ![]() ,解得交点坐标为A(1,0),B(
,解得交点坐标为A(1,0),B( ![]() ,﹣
,﹣ ![]() )
)
所以|AB|= ![]() =1;
=1;
(II)曲线C2: 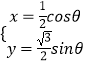 (θ为参数).
(θ为参数).
设所求的点为P( ![]() cosθ,
cosθ, ![]() sinθ),
sinθ),
则P到直线l的距离d= ![]() =
= ![]() [
[ ![]() sin(
sin( ![]() )+2]
)+2]
当sin( ![]() )=﹣1时,d取得最小值
)=﹣1时,d取得最小值 ![]()
【解析】(I)将直线l中的x与y代入到直线C1中,即可得到交点坐标,然后利用两点间的距离公式即可求出|AB|.(II)将直线的参数方程化为普通方程,曲线C2任意点P的坐标,利用点到直线的距离公式P到直线的距离d,分子合并后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,与分母约分化简后,根据正弦函数的值域可得正弦函数的最小值,进而得到距离d的最小值即可.
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识,掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为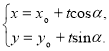 (
(![]() 为参数),以及对圆的参数方程的理解,了解圆
为参数),以及对圆的参数方程的理解,了解圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目