题目内容
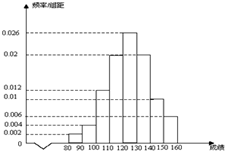 某学科在市模考后从全年级抽出100名学生的学科成绩作为样本进行分析,得到样本频率分布直方图如图所示.
某学科在市模考后从全年级抽出100名学生的学科成绩作为样本进行分析,得到样本频率分布直方图如图所示.(1)求该学科学生成绩在[100,130]之间的人数;
(2)估计该次考试该学科的中位数和平均分.
分析:(1)根据图形计算成绩在100到130之间小矩形的面积求出频率,再乘以样本容量可求出所求;
(2)根据中位数的左右两边矩形面积相等,来求中位数;由频率分步直方图知用每组的中间值作为每组中的样本数据,直接计算平均成绩.
(2)根据中位数的左右两边矩形面积相等,来求中位数;由频率分步直方图知用每组的中间值作为每组中的样本数据,直接计算平均成绩.
解答:解:(1)由统计图知,由图可知样本中成绩在100到130之间的学生有100×(0.12+0.2+0.26)=58人,样本容量为100,
∴样本中成绩在100~130之间的学生有58人.
(2)∵前四个小长方形的面积和为0.02+0.04+0.12+0.2=0.38,设0.38+0.026×x=0.5,
解得x=4.6,
∴中位数是124.6,
样本的平均数为85×0.02+95×0.04+105×0.12+115×0.2+125×0.26+135×0.2+145×0.1+155×0.06=124.4,
∴本次考试平均成绩为124.4.
∴样本中成绩在100~130之间的学生有58人.
(2)∵前四个小长方形的面积和为0.02+0.04+0.12+0.2=0.38,设0.38+0.026×x=0.5,
解得x=4.6,
∴中位数是124.6,
样本的平均数为85×0.02+95×0.04+105×0.12+115×0.2+125×0.26+135×0.2+145×0.1+155×0.06=124.4,
∴本次考试平均成绩为124.4.
点评:本题考查了利用样本的频率分布直方图估计中位数,平均数,考查了利用频率分布直方图求概率,从频率分布直方图中获取的相关的数据,并正确的处理解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
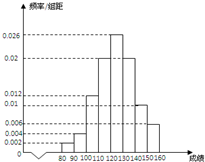 某学科在市模考后从全年级抽出100名学生的学科成绩作为样本进行分析,得到样本频率分布直方图如图所示.
某学科在市模考后从全年级抽出100名学生的学科成绩作为样本进行分析,得到样本频率分布直方图如图所示.