Question

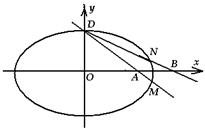已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)短轴的一个端点D(0，

3

)，离心率e=

1

2

．过D作直线l与椭圆交于另一点M，与x轴交于点A（不同于原点O），点M关于x轴的对称点为N，直线DN交x轴于点B．
（Ⅰ）求椭圆的方程；
（Ⅱ）求|

OA

|•|

OB

|的值．

Answer 1

分析：（Ⅰ）根据题意，短轴的端点坐标，可得b=

3

，又由离心率e=

1

2

，则a=2c，代入a²=b²+c²中；解可得a、b的值，即可得答案．
（Ⅱ）设直线l方程为y=kx+

3

．令y=0，得A的坐标；进而联立方程组

y=kx+ 3 3x2+4y2=12

，可得M、N两点的坐标，进而可得直线DN的方程，即可得B的坐标，进而由数量积的公式，计算可得答案．

解答：解：（Ⅰ）由已知，短轴的一个端点D(0，

3

)，则b=

3

；
离心率e=

1

2

，则a=2c，
又由a²=b²+c²；
解可得a=2，b=

3

．
所以椭圆方程为

x2

4

+

y2

3

=1．
（Ⅱ）设直线l方程为y=kx+

3

．令y=0，得A(-

3

k

，0)．
由方程组

y=kx+ 3 3x2+4y2=12

可得3x2+4(kx+

3

)2=12，即(3+4k2)x2+8

3

kx=0．
所以xM=-

8 3 k

3+4k2

，
所以M(-

8 3 k

3+4k2

，-

8 3 k2

3+4k2

+

3

)，N(-

8 3 k

3+4k2

，

8 3 k2

3+4k2

-

3

)．
所以kDN=

2 3 - 8 3 k2 3+4k2

8 3 k 3+4k2

=

3

4k

．
直线DN的方程为y=

3

4k

x+

3

．
令y=0，得B(-

4 3 k

3

，0)．
所以|

OA

|•|

OB

|=|-

4 3 k

3

|•|-

3

k

|=4．

点评：本题考查直线与椭圆的关系，是一道综合题；解题时，注意充分利用题干的条件，从中提取有关的信息，起到简化计算步骤，降低运算量的目的．