题目内容
甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分.若甲、乙两名同学射击的命中率分别为| 3 |
| 5 |
| 9 |
| 20 |
(1)求p的值;
(2)记甲、乙两人各射击一次所得分数之和为ξ,求ξ的分布列和数学期望.
分析:(1)由题意知甲、乙两人射击互不影响,则本题是一个相互独立事件同时发生的概率,根据甲、乙两人各射击一次所得分数之和为2的概率为
,写出关于p的方程,解方程求的结果.
(2)甲、乙两人各射击一次所得分数之和为ξ,根据题意知变量的可能取值是0、2、4,结合变量对应的事件写出概率和分布列,求出期望.
| 9 |
| 20 |
(2)甲、乙两人各射击一次所得分数之和为ξ,根据题意知变量的可能取值是0、2、4,结合变量对应的事件写出概率和分布列,求出期望.
解答:解:(1)设“甲射击一次,击中目标”为事件A,
“乙射击一次,击中目标”为事件B,
“甲射击一次,未击中目标”为事件
,
“乙射击一次,未击中目标”为事件
,
则P(A)=
,P(
)=
,P(B)=P,P(
)=1-P
依题意得:
(1-P)+
P=
,
解得P=
,
故p的值为
.
(2)ξ的取值分别为0,2,4.
P(ξ=0)=P(
)=P(
)P(
)=
×
=
,
P(ξ=2)=
P(ξ=4)=P(AB)=P(A)P(B)=
×
=
,
∴ξ的分布列为

∴Eξ=0×
+2×
+4×
=
“乙射击一次,击中目标”为事件B,
“甲射击一次,未击中目标”为事件
. |
| A |
“乙射击一次,未击中目标”为事件
. |
| B |
则P(A)=
| 3 |
| 5 |
. |
| A |
| 2 |
| 5 |
. |
| B |
依题意得:
| 3 |
| 5 |
| 2 |
| 5 |
| 9 |
| 20 |
解得P=
| 3 |
| 4 |
故p的值为
| 3 |
| 4 |
(2)ξ的取值分别为0,2,4.
P(ξ=0)=P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 2 |
| 5 |
| 1 |
| 4 |
| 1 |
| 10 |
P(ξ=2)=
| 9 |
| 20 |
P(ξ=4)=P(AB)=P(A)P(B)=
| 3 |
| 5 |
| 3 |
| 4 |
| 9 |
| 20 |
∴ξ的分布列为

∴Eξ=0×
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 10 |
点评:考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.

练习册系列答案
相关题目
 和p,且甲、乙两人各射击一次所得分数之和为2的概率为
和p,且甲、乙两人各射击一次所得分数之和为2的概率为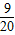 ,假设甲、乙两人射击互不影响
,假设甲、乙两人射击互不影响 和p,且甲、乙两人各射击一次所得分数之和为2的概率为
和p,且甲、乙两人各射击一次所得分数之和为2的概率为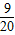 ,假设甲、乙两人射击互不影响
,假设甲、乙两人射击互不影响