题目内容
在等差数列{an}中,已知a1+a2+a3=9,a2+a4+a6=21。
(1)求数列{an}的通项公式;
(2)设bn=2n·an,求数列{bn}的前n项和Sn。
(1)求数列{an}的通项公式;
(2)设bn=2n·an,求数列{bn}的前n项和Sn。
解:(1)在等差数列{an}中,由a1+a2+a3=3a2=9,得a2=a1+d=3
又由a2+a4+a6=3a4=21,得a4=a1+3d=7
联立解得a1=1,d=2,
则数列{an}的通项公式为an=2n-1。
(2)因为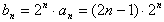
∴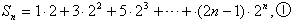
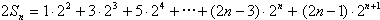 ②
②
①-②得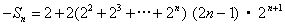
得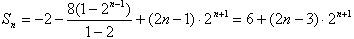 。
。
又由a2+a4+a6=3a4=21,得a4=a1+3d=7
联立解得a1=1,d=2,
则数列{an}的通项公式为an=2n-1。
(2)因为
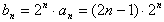
∴
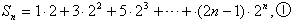
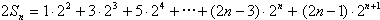 ②
②①-②得
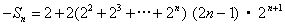
得
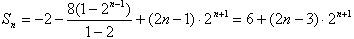 。
。
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目