题目内容
已知函数f(x)=ln(x+1)-ax+ (a≥
(a≥ ),
),
(1)当曲线y=f(x)在点(1,f(1))处的切线与直线l:y=-2x+1平行时,求a的值;
(2)求函数f(x)的单调区间。
 (a≥
(a≥ ),
),(1)当曲线y=f(x)在点(1,f(1))处的切线与直线l:y=-2x+1平行时,求a的值;
(2)求函数f(x)的单调区间。
解: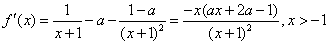 ,
,
(1)由题意可得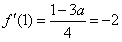 ,解得a=3,
,解得a=3,
因为f(1)=ln2-4,此时在点(1,f(1))处的切线方程为y-(ln2-4)=-2(x-1),即y=-2x+ln2-2,
与直线l:y=-2x+1平行,故所求a的值为3.
(2)令f′(x)=0,得到 ,
,
由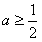 可知
可知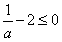 ,即x1≤0,
,即x1≤0,
①当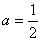 时,
时,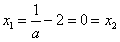 ,
,
所以,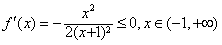 ,
,
故f(x)的单调递减区间为(-1,+∞).
②当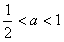 时,
时,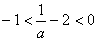 ,即-1<x1<0=x2,
,即-1<x1<0=x2,
所以,在区间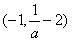 和(0,+∞)上,f′(x)<0;
和(0,+∞)上,f′(x)<0;
在区间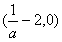 上,f′(x)>0,
上,f′(x)>0,
故f(x)的单调递减区间是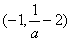 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是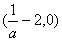 ;
;
③当a≥1时,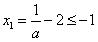 ,
,
所以,在区间(-1,0)上,f′(x)>0;在区间(0,+∞)上,f′(x)<0,
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞);
综上讨论可得:当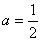 时,函数f(x)的单调递减区间是(-1,+∞);
时,函数f(x)的单调递减区间是(-1,+∞);
当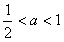 时,函数f(x)的单调递减区间是
时,函数f(x)的单调递减区间是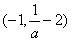 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是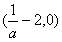 ;
;
当a≥1时,函数f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞).
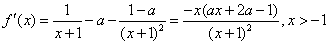 ,
,(1)由题意可得
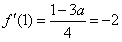 ,解得a=3,
,解得a=3,因为f(1)=ln2-4,此时在点(1,f(1))处的切线方程为y-(ln2-4)=-2(x-1),即y=-2x+ln2-2,
与直线l:y=-2x+1平行,故所求a的值为3.
(2)令f′(x)=0,得到
 ,
,由
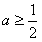 可知
可知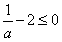 ,即x1≤0,
,即x1≤0,①当
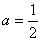 时,
时,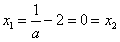 ,
,所以,
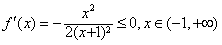 ,
,故f(x)的单调递减区间为(-1,+∞).
②当
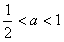 时,
时,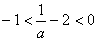 ,即-1<x1<0=x2,
,即-1<x1<0=x2,所以,在区间
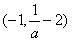 和(0,+∞)上,f′(x)<0;
和(0,+∞)上,f′(x)<0;在区间
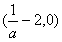 上,f′(x)>0,
上,f′(x)>0,故f(x)的单调递减区间是
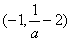 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是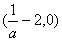 ;
;③当a≥1时,
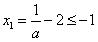 ,
,所以,在区间(-1,0)上,f′(x)>0;在区间(0,+∞)上,f′(x)<0,
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞);
综上讨论可得:当
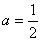 时,函数f(x)的单调递减区间是(-1,+∞);
时,函数f(x)的单调递减区间是(-1,+∞);当
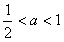 时,函数f(x)的单调递减区间是
时,函数f(x)的单调递减区间是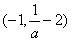 和(0,+∞),单调递增区间是
和(0,+∞),单调递增区间是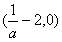 ;
;当a≥1时,函数f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞).

练习册系列答案
相关题目