题目内容
过坐标原点且与x2+y2 -4x+2y+
=0相切的直线的方程为 （ ）
A．y=-3x或y= x |
| B．y=-3x或y=-x |
C．y=-3x或y =-x |
| D．y=3x或y=x |
A
解析
练习册系列答案
相关题目
函数
的导函数
在区间
上的图象大致是（ ）
A． | B． |
C． | D． |
如图，函数
与
相交形成一个闭合图形(图中的阴影部分)，
则该闭合图形的面积是( )
| A．2 | B． |
C． | D．1 |
设
，若函数
的极值点小于零，则（ ）
A． | B． | C． | D． |
函数
的定义域为
，
，对任意
则
的解集为
| A．（-1，1） | B．（-1，+ ） | C．(-,-1) | D． (- ) |
若函数
在
内有极小值，则实数
的取值范围是
| A． | B． | C． | D． |
已知曲线y=
x3+
，则过点P（2
，4）的切线方程是 （ ）
| A．4x－y－4="0." | B．x－4y－4=0 . |
| C．4x－4y－1="0." | D．4x+y－4=0. |
若函数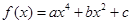
满足
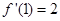，则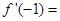
（ ）
A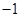． | B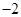． | C．2 | D．0 |