题目内容
6.如果函数y=a2x+2ax-1(a>0,a≠1)在区间[-1,1]上的最大值是14,则实数a的值为3或$\frac{1}{3}$.分析 令t=ax,结合指数函数和一元二次函数的性质进行求解即可.
解答 解:设t=ax,则函数等价为y=f(t)=t2+2t-1=(t+1)2-2,
对称轴为t=-1,
若a>1,则0<$\frac{1}{a}$≤t≤a,
此时函数的最大值为f(a)=(a+1)2-2=14,即(a+1)2=16,
即a+1=4或a+1=-4,
即a=3或a=-5(舍),
若0<a<1,则0<a≤t≤$\frac{1}{a}$,
此时函数的最大值为f($\frac{1}{a}$)=($\frac{1}{a}$+1)2-2=14,即($\frac{1}{a}$+1)2=16,
即$\frac{1}{a}$+1=4或$\frac{1}{a}$+1=-4,
即$\frac{1}{a}$=3或$\frac{1}{a}$=-5(舍),
解得a=$\frac{1}{3}$,
综上3或$\frac{1}{3}$;
故答案为:3或$\frac{1}{3}$;
点评 本题主要考查指数函数的性质和应用,利用换元法结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
14.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,则(a-c)2+(b-d)2的最小值为( )
| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
11.化简lg$\sqrt{2}$+lg$\sqrt{5}$+log31的结果是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{10}$ |
18.甲、乙两人参加某单位招聘面试测试,每次测试从试题库随机用一套试题,他们参加的5项测试成绩记录如下:
(1)用茎叶图表示甲、乙这5项测试成绩;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
16.已知$tanα=\frac{1}{2}$,则$\frac{{2{{cos}^2}\frac{α}{2}-sinα-1}}{{\sqrt{2}sin(\frac{π}{4}+α)}}$的值为( )
| A. | $\frac{4}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
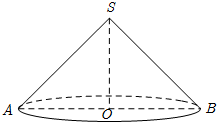 如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.
如图,已知圆锥的轴截面SAB是等腰直角三角形,且该圆锥体积为$\frac{8}{3}$π,求该圆锥的表面积.