Question

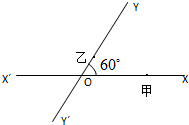如图，有两条相交成60°的直路XX′，YY′，交点是O，甲、乙分别在OX，OY上，起初甲离O点3km，乙离O点1km，后甲沿XX′方向用2km/h的速度，乙沿Y′Y方向用4km/h的速度同时步行．设t小时后甲在XX′上点A处，乙在YY′上点B处．
（Ⅰ）求t=1.5时，甲、乙两人之间的距离；
（Ⅱ）求t=2时，甲、乙两人之间的距离；
（Ⅲ） 当t为何值时，甲、乙两人之间的距离最短？

Answer 1

分析：（I）当t=1.5时，甲运动到点O，而乙运动了6km，故可求甲、乙之间的距离；
（Ⅱ）当t=2时，点A在直线XX′上O点左侧距离O 点1km处，而点B在直线YY′上O点上方距离O点9km处，利用余弦定理，可得结论；
（III）分类讨论，利用余弦定理，配方法，即可得出结论．

解答：解：（Ⅰ）当t=1.5时，甲运动到点O，而乙运动了6km，故这时甲、乙之间的距离为7．…（4分）
（Ⅱ）当t=2时，点A在直线XX′上O点左侧距离O 点1km处，而点B在直线YY′上O点上方距离O点9km处，这时∠AOB=60°，所以，由余弦定理得AB=

12+92-2×1×9×cos120°

=

91

（km）…（8分）
（Ⅲ）当0＜t≤

3

2

时，AB=

(3-2t)2+(1+4t)2-2(3-2t)(1+4t)cos60°

=

28t2-14t+7

   …（10分）
当t＞

3

2

时，AB=

(2t-3)2+(1+4t)2-2(2t-3)(1+4t)cos120°

=

28t2-14t+7

 …（12分）
∴t小时后，甲、乙两人的距离为

28t2-14t+7

km
∵

28t2-14t+7

=

28(t- 1 4 )2+ 21 4

∴当t=

1

4

小时，甲、乙两人的距离最短．               …（14分）

点评：本题考查学生根据实际问题选择函数类型的能力，考查了余弦定理，熟练掌握余弦定理是解本题的关键．