题目内容
已知数列{an}的前n项和为Sn,且-1,Sn,an+1成等差数列,n∈N*,a1=1.函数f(x)=log3x.
(I)求数列{an}的通项公式;
(II)设数列{bn}满足bn=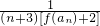 ,记数列{bn}的前n项和为Tn,试比较Tn与
,记数列{bn}的前n项和为Tn,试比较Tn与 -
-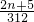 的大小.
的大小.
解:(I)∵-1,Sn,an+1成等差数列,
∴2Sn=an+1-1①
当n≥2时,2Sn-1=an-1②.
①-②得:2an=an+1-an,
∴ =3.
=3.
当n=1时,由①得2S1=2a1=a2-1,又a1=1,
∴a2=3,故 =3.
=3.
∴{an}是以1为首项3为公比的等比数列,
∴an=3n-1…(7分)
(II)∵f(x)=log3x,
∴f(an)=log3an=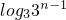 =n-1,
=n-1,
bn=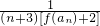 =
=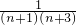 =
= (
( -
-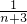 ),
),
∴Tn= [(
[( -
- )+(
)+( -
- )+…+(
)+…+( -
-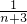 )]
)]
= (
( +
+ -
- -
-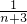 )
)
= -
-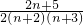 …(9分)
…(9分)
比较Tn与 -
-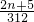 的大小,只需比较2(n+2)(n+3)与312 的大小即可.…(10分)
的大小,只需比较2(n+2)(n+3)与312 的大小即可.…(10分)
2(n+2)(n+3)-312=2(n2+5n+6-156)=2(n2+5n+-150)=2(n+15)(n-10),
∵n∈N*,
∴当1≤n≤9时,2(n+2)(n+3)<312,即Tn< -
-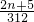 ;
;
当n=10时,2(n+2)(n+3)=312,即Tn= -
-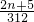 ;
;
当n>10且n∈N*时,2(n+2)(n+3)>312,即Tn> -
-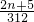 .…(14分)
.…(14分)
分析:(I)依题意可求得 =3( n≥2),再由2S1=2a1=a2-1,a1=1即可求得{an}是以1为首项3为公比的等比数列,从而可求数列{an}的通项公式;
=3( n≥2),再由2S1=2a1=a2-1,a1=1即可求得{an}是以1为首项3为公比的等比数列,从而可求数列{an}的通项公式;
(II)依题意可求得bn= (
( -
-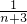 ),利用累加法可求得Tn,从而通过分类讨论即可比较Tn与
),利用累加法可求得Tn,从而通过分类讨论即可比较Tn与 -
-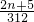 的大小.
的大小.
点评:本题考查数列的求和,突出考查裂项法求和,着重考查分类讨论思想与转化思想的综合应用,属于难题.
∴2Sn=an+1-1①
当n≥2时,2Sn-1=an-1②.
①-②得:2an=an+1-an,
∴
 =3.
=3.当n=1时,由①得2S1=2a1=a2-1,又a1=1,
∴a2=3,故
 =3.
=3.∴{an}是以1为首项3为公比的等比数列,
∴an=3n-1…(7分)
(II)∵f(x)=log3x,
∴f(an)=log3an=
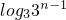 =n-1,
=n-1,bn=
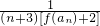 =
=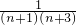 =
= (
( -
-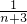 ),
),∴Tn=
 [(
[( -
- )+(
)+( -
- )+…+(
)+…+( -
-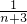 )]
)]=
 (
( +
+ -
- -
-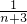 )
)=
 -
-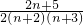 …(9分)
…(9分)比较Tn与
 -
-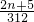 的大小,只需比较2(n+2)(n+3)与312 的大小即可.…(10分)
的大小,只需比较2(n+2)(n+3)与312 的大小即可.…(10分)2(n+2)(n+3)-312=2(n2+5n+6-156)=2(n2+5n+-150)=2(n+15)(n-10),
∵n∈N*,
∴当1≤n≤9时,2(n+2)(n+3)<312,即Tn<
 -
-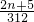 ;
;当n=10时,2(n+2)(n+3)=312,即Tn=
 -
-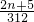 ;
;当n>10且n∈N*时,2(n+2)(n+3)>312,即Tn>
 -
-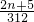 .…(14分)
.…(14分)分析:(I)依题意可求得
 =3( n≥2),再由2S1=2a1=a2-1,a1=1即可求得{an}是以1为首项3为公比的等比数列,从而可求数列{an}的通项公式;
=3( n≥2),再由2S1=2a1=a2-1,a1=1即可求得{an}是以1为首项3为公比的等比数列,从而可求数列{an}的通项公式;(II)依题意可求得bn=
 (
( -
-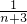 ),利用累加法可求得Tn,从而通过分类讨论即可比较Tn与
),利用累加法可求得Tn,从而通过分类讨论即可比较Tn与 -
-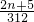 的大小.
的大小.点评:本题考查数列的求和,突出考查裂项法求和,着重考查分类讨论思想与转化思想的综合应用,属于难题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |