题目内容
已知函数f(x)=(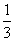 )x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a)。
)x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a)。
(1)求h(a);
(2)是否存在实数m,n,同时满足以下条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]。若存在,求出m,n的值;若不存在,说明理由.
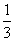 )x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a)。
)x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a)。(1)求h(a);
(2)是否存在实数m,n,同时满足以下条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]。若存在,求出m,n的值;若不存在,说明理由.
解:(1)因为x∈[-1,1],所以 ,
,
设 ,
,
则g(x)=φ(t)=t2-2at+3=(t-a)2+3-a2,
当a< 时,
时, ;
;
当 ≤a≤3时,h(a)=φ(a)=3-a2;
≤a≤3时,h(a)=φ(a)=3-a2;
当a>3时,h(a)=φ(3)=12-6a;
所以, 。
。
(2)因为m>n>3,a∈[n,m],所以h(a)=12-6a,
因为h(a)的定义域为[n,m],值域为[n2,m2],且h(a)为减函数,
所以 ,两式相减得6(m-n)=(m-n)(m+n),
,两式相减得6(m-n)=(m-n)(m+n),
因为m>n,所以m-n≠0,得m+n=6,
但这与“m>n>3”矛盾,故满足条件的实数m,n不存在。
 ,
,设
 ,
, 则g(x)=φ(t)=t2-2at+3=(t-a)2+3-a2,
当a<
 时,
时, ;
; 当
 ≤a≤3时,h(a)=φ(a)=3-a2;
≤a≤3时,h(a)=φ(a)=3-a2;当a>3时,h(a)=φ(3)=12-6a;
所以,
 。
。(2)因为m>n>3,a∈[n,m],所以h(a)=12-6a,
因为h(a)的定义域为[n,m],值域为[n2,m2],且h(a)为减函数,
所以
 ,两式相减得6(m-n)=(m-n)(m+n),
,两式相减得6(m-n)=(m-n)(m+n),因为m>n,所以m-n≠0,得m+n=6,
但这与“m>n>3”矛盾,故满足条件的实数m,n不存在。

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|