题目内容
已知函数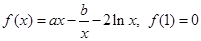
(Ⅰ)若函数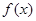 在其定义域上为单调函数,求
在其定义域上为单调函数,求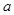 的取值范围;
的取值范围;
(Ⅱ)若函数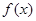 的图像在
的图像在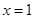 处的切线的斜率为0,
处的切线的斜率为0,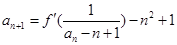 ,已知
,已知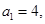 求证:
求证: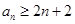
(Ⅲ)在(2)的条件下,试比较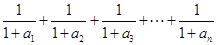 与
与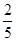 的大小,并说明理由.
的大小,并说明理由.
【答案】
(Ⅰ)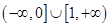 ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)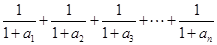 <
<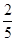 .
.
【解析】
试题分析:(Ⅰ)利用导数求解单调性,把恒成立转化为最值;(Ⅱ)可用数学归纳法来证明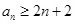 ;(Ⅲ)通过放缩法来解决
;(Ⅲ)通过放缩法来解决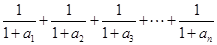 与
与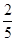 的大小比较问题.
的大小比较问题.
试题解析:(Ⅰ) ∵f(1)=a-b=0 ∴a=b
∴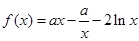
∴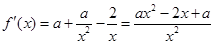
要使函数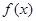 在其定义域上为单调函数,则在定义域(0,+∞)内
在其定义域上为单调函数,则在定义域(0,+∞)内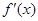 恒大于等于0或恒小于等于0,
恒大于等于0或恒小于等于0,
当a=0时,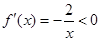 在(0,+∞)内恒成立;
在(0,+∞)内恒成立;
当a>0时,
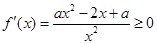 恒成立,则
恒成立,则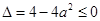 ∴
∴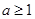
当a<0时,
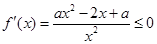 恒成立
恒成立
∴a的取值范围是: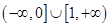 5分
5分
(Ⅱ) 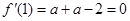 ∴a=1 则:
∴a=1 则: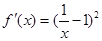
于是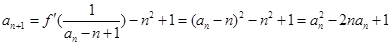
用数学归纳法证明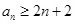 如下:
如下:
当n=1时,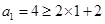 ,不等式成立;
,不等式成立;
假设当n=k时,不等式 成立,即
成立,即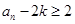 也成立,
也成立,
当n=k+1时,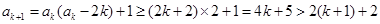
所以当n=k+1时不等式成立,
综上得对所有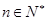 时,都有
时,都有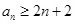 10分
10分
(Ⅲ)由(2)得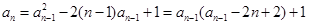
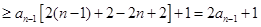
于是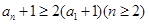
所以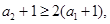
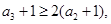 ,
,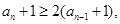
累称得: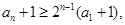 则
则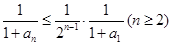
所以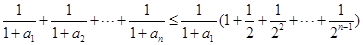
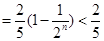 13分
13分
考点:利用导数处理单调性,数列中的数学归纳法、放缩法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
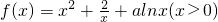 ,
,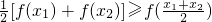 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.