题目内容
设函数 的定义域为集合A,函数
的定义域为集合A,函数 (a>0)的定义域为集合B.
(a>0)的定义域为集合B.
(1)当a=1时,求集合A∩B;
(2)若A∩B=B,求实数a的取值范围.
解:(1)由函数 有意义,
有意义,
得: ,
,
即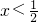 或
或 ,
,
所以 ,
,
当a=1时,函数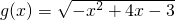 有意义,
有意义,
得:-x2+4x-3≥0,
即x2-4x+3≤0,
∴1≤x≤3,∴B={x|1≤x≤3},
∴
(2)由函数 (a>0)有意义得-x2+4x-3a2≥0,
(a>0)有意义得-x2+4x-3a2≥0,
即(x-a)(x-3a)≤0,
∵a>0,∴a≤x≤3a,
∴B=[a,3a],
若A∩B=B,则B⊆A,
∴ 或
或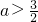 ,得
,得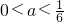 或
或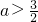 ,
,
即
分析:(1)由函数 有意义,得
有意义,得 ,当a=1时,函数
,当a=1时,函数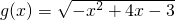 有意义,得B={x|1≤x≤3},由此能求出当a=1时集合A∩B.
有意义,得B={x|1≤x≤3},由此能求出当a=1时集合A∩B.
(2)由函数 (a>0)有意义得B=[a,3a],由A∩B=B,知B⊆A,由此能求出实数a的取值范围.
(a>0)有意义得B=[a,3a],由A∩B=B,知B⊆A,由此能求出实数a的取值范围.
点评:本题考查集合的交集和集合的包含关系的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
 有意义,
有意义,得:
 ,
,即
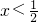 或
或 ,
,所以
 ,
,当a=1时,函数
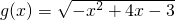 有意义,
有意义,得:-x2+4x-3≥0,
即x2-4x+3≤0,
∴1≤x≤3,∴B={x|1≤x≤3},
∴

(2)由函数
 (a>0)有意义得-x2+4x-3a2≥0,
(a>0)有意义得-x2+4x-3a2≥0,即(x-a)(x-3a)≤0,
∵a>0,∴a≤x≤3a,
∴B=[a,3a],
若A∩B=B,则B⊆A,
∴
 或
或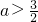 ,得
,得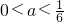 或
或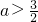 ,
,即

分析:(1)由函数
 有意义,得
有意义,得 ,当a=1时,函数
,当a=1时,函数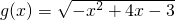 有意义,得B={x|1≤x≤3},由此能求出当a=1时集合A∩B.
有意义,得B={x|1≤x≤3},由此能求出当a=1时集合A∩B.(2)由函数
 (a>0)有意义得B=[a,3a],由A∩B=B,知B⊆A,由此能求出实数a的取值范围.
(a>0)有意义得B=[a,3a],由A∩B=B,知B⊆A,由此能求出实数a的取值范围.点评:本题考查集合的交集和集合的包含关系的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
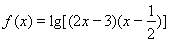

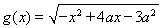
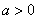

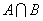
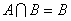
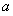
 .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围. 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。 ,求实数
,求实数 的取值范围。
的取值范围。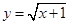 的定义域为集合
的定义域为集合 ,不等式
,不等式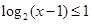 的解集为集合
的解集为集合 .
.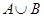 ,
,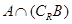 .
.