题目内容

设关于x的方程ax2-bx+c=0中a、b、c是钝角三角形的边,b最大,证明这个方程有相异的正实根.

      

思路分析:证明方程有两个相异的正实根,要从两方面入手:一方面证方程有两个相异实根,一方面证两根均为正.可考虑使用判别式和韦达定理.?

       证明:∵关于x的方程ax2-bx+c=0,?

       Δ=b2-4ac=(-b)2-4ac=2b2-4ac.?

       又∵a、b、c是钝角三角形的三边,b最大,?

       ∴b2>a2+c2≥2ac,∴b2-2ac>0.?

       ∴Δ=2(b2-2ac)>0.?

       ∴方程有两个相异实根.?

       又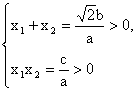(a、b、c为三角形的边),?

       ∴两根均为正根.?

       ∴原结论成立.

练习册系列答案
相关题目
已知f（x）=4x+ax2-
2
3
x3(x∈R)在区间[-1，1]上是增函数．
（Ⅰ）求实数a的值组成的集合A；
（Ⅱ）设关于x的方程f（x）=2x+
1
3
x3的两个非零实根为x1、x2．试问：是否存在实数m，使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由．
（2012•绍兴一模）设
a
、
b
、
c
是三个非零向量，且
a
、
b
不共线，若关于x的方程
a
x2+
b
x+
c
=
0
的两个根为x1，x2，则（　　）
（2010•广东模拟）已知函数f(x)=4x+ax2-
2
3
x3(x∈R)．
（1）若a=1，求函数f（x）的单调区间；
（2）若函数f（x）在区间[-1，1]上单调递增，求实数a的取值组成的集合A；
（3）设关于x的方程f(x)=2x+
1
3
x3的两个非零实根为x1，x2，试问是否存在实数m，使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1，1]恒成立？若存在，求出m的取值范围；若不存在，请说明理由．
设关于x的方程2x2-ax-2=0的两根为α，β（α＜β），函数f(x)=
4x-ax2+1
，且|f（α）•f（β）|=4．
（1）证明：f（x）在[α，β]上是增函数；
（2）当α为何值时，f（x）在[α，β]上的最大值与最小值之差最小？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网