题目内容
设{an}是有正数组成的等比数列,Sn为其前n项和.已知a2a4=1,S3=7,则S5=( )A.
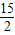
B.
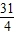
C.
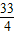
D.
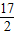
【答案】分析:先由等比中项的性质求得a3,再利用等比数列的通项求出公比q及首项a1,最后根据等比数列前n项和公式求得S5.
解答:解:由a2a4=a32=1,得a3=1,
所以S3=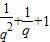 =7,
=7,
又q>0,解得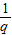 =2,即q=
=2,即q= .
.
所以a1=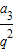 =4,
=4,
所以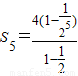 =
=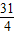 .
.
故选B.
点评:本题考查等比中项的性质、等比数列的通项公式及前n项和公式.
解答:解:由a2a4=a32=1,得a3=1,
所以S3=
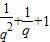 =7,
=7,又q>0,解得
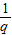 =2,即q=
=2,即q= .
.所以a1=
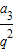 =4,
=4,所以
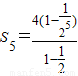 =
=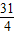 .
.故选B.
点评:本题考查等比中项的性质、等比数列的通项公式及前n项和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
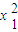 +
+ +…+
+…+ ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B; +
+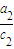 +
+ 的最小值为3;
的最小值为3; +
+ +…+
+…+ +
+ 的最小值为
的最小值为 .
.