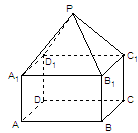
题目内容
如图,在直三棱柱 中,
中,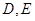 分别为
分别为 、
、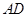 的中点,
的中点, 为
为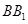 上的点,且
上的点,且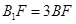
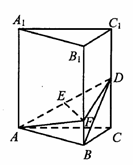
(I)证明: ∥平面
∥平面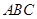 ;
;
(Ⅱ)若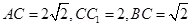 ,
, ,求三棱锥
,求三棱锥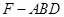 的体积.
的体积.
(I) 平面
平面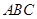 ;(II)
;(II) .
.
解析试题分析:(I)取线段 的中点
的中点 ,证明平面
,证明平面 ∥平面
∥平面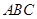 ,就可以证明
,就可以证明 平面
平面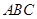 ;
;
(II)根据 以及余弦定理求出
以及余弦定理求出 ,而
,而 ,所以
,所以 ,
, 平面
平面 ,那么就可以根据等体积公式得到
,那么就可以根据等体积公式得到 .
.
试题解析:(I)取线段 的中点
的中点 ,并连接
,并连接 、
、 ,则
,则 ,
, ,
,

 ,
, ,
, 平面
平面 平面
平面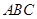
 平面
平面 ,
,
 平面
平面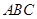 .
.
(II)已知 ,由余弦定理知
,由余弦定理知 ,解得
,解得 ,而
,而 ,所以
,所以 ,
, ,
, 平面
平面 .
. .
.
考点:1.线面平行的证明;2.三棱锥体积的计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
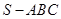 中,
中,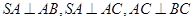 且
且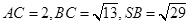 .
.
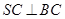 ;
;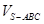 .
.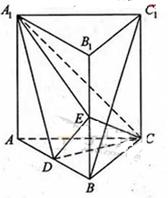
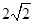 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.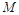 是
是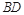 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.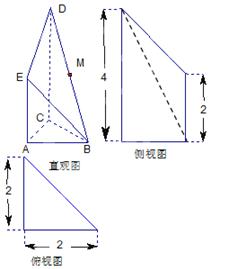
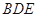 ? 若存在,确定
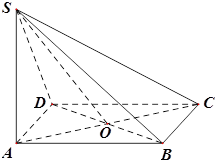
? 若存在,确定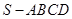 中,侧棱
中,侧棱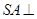 底面
底面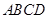 ,且底面
,且底面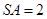 ,
,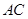 与
与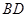 相交于点
相交于点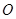 .
.
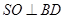 ;
;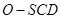 的体积.
的体积.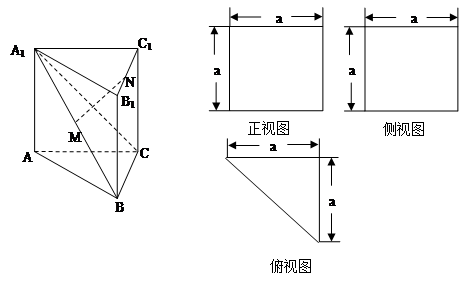
 ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.
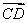 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)