题目内容
3.设$\overrightarrow a$=($\frac{3}{4}$,sinα),$\overrightarrow b$=(cosα,$\frac{1}{4}$)且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则tanα=-3.分析 通过化简可得$\frac{1}{4}$sinα+$\frac{3}{4}$cosα=0,进而可得tanα的值.
解答 解:∵$\overrightarrow a$=($\frac{3}{4}$,sinα),$\overrightarrow b$=(cosα,$\frac{1}{4}$)且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=($\frac{3}{4}$,sinα)•(cosα,$\frac{1}{4}$)=$\frac{1}{4}$sinα+$\frac{3}{4}$cosα=0,
∴$\frac{sinα}{cosα}$=$\frac{3}{1}$,即tanα=-3,
故答案为:-3.
点评 本题考查平面向量数量积的运算,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
8.运行如图的程序框图,若输入n=2015,则输出的a=( )
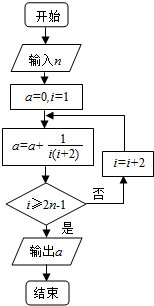

| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
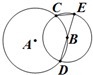 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.