题目内容
已知函数f(x)=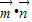 ,其中
,其中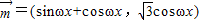 ,
,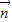 =(cosωx-sinωx,2sinωx),其中ω>0,若f(x)相邻两对称轴间的距离不小于
=(cosωx-sinωx,2sinωx),其中ω>0,若f(x)相邻两对称轴间的距离不小于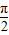 .
.(Ⅰ)求ω的取值范围;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=
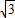 ,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
,b+c=3,当ω最大时,f(A)=1,求△ABC的面积.
【答案】分析:(I)利用向量的数量积的坐标表示及二倍角公式对函数整理可得,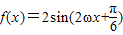 ,根据周期公式可得
,根据周期公式可得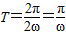 ,根据正弦函数的性质相邻两对称轴间的距离即为
,根据正弦函数的性质相邻两对称轴间的距离即为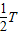 ,从而有
,从而有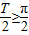 代入可求ω的取值范围.
代入可求ω的取值范围.
(Ⅱ)由(Ⅰ)可知ω的最大值为1,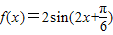 由f(A)=1可得,
由f(A)=1可得,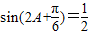 结合已知可得
结合已知可得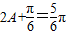 ,
,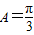 由余弦定理知
由余弦定理知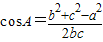 可得b2+c2-bc=3,又b+c=3联立方程可求b,c,代入面积公式可求
可得b2+c2-bc=3,又b+c=3联立方程可求b,c,代入面积公式可求
也可用配方法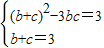 求得bc=2,直接代入面积公式可求
求得bc=2,直接代入面积公式可求
解答:解:(Ⅰ)f(x)=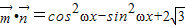
cosωx•sinωx=cos2ωx+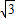 sin2ωx=
sin2ωx=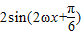
∵ω>0
∴函数f(x)的周期T=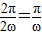 ,由题意可知
,由题意可知 ,
,
解得0<ω≤1,即ω的取值范围是{ω|0<ω≤1}
(Ⅱ)由(Ⅰ)可知ω的最大值为1,
∴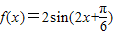
∵f(A)=1
∴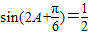
而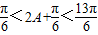 π
π
∴2A+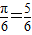 π
π
∴A=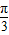
由余弦定理知cosA=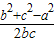
∴b2+c2-bc=3,又b+c=3
联立解得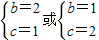
∴S△ABC=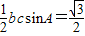
(或用配方法∵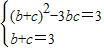
∴bc=2
∴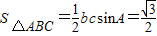 .
.
点评:本题综合考查了向量的数量积的坐标表示,由函数的部分图象的性质求解函数的解析式,正弦函数的周期公式,由三角函数值求解角,余弦定理及三角形的面积公式等知识的综合,综合的知识比较多,解法灵活,要求考生熟练掌握基础知识并能灵活运用知识进行解题.
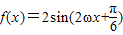 ,根据周期公式可得
,根据周期公式可得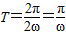 ,根据正弦函数的性质相邻两对称轴间的距离即为
,根据正弦函数的性质相邻两对称轴间的距离即为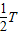 ,从而有
,从而有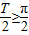 代入可求ω的取值范围.
代入可求ω的取值范围.(Ⅱ)由(Ⅰ)可知ω的最大值为1,
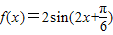 由f(A)=1可得,
由f(A)=1可得,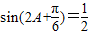 结合已知可得
结合已知可得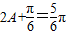 ,
,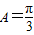 由余弦定理知
由余弦定理知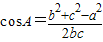 可得b2+c2-bc=3,又b+c=3联立方程可求b,c,代入面积公式可求
可得b2+c2-bc=3,又b+c=3联立方程可求b,c,代入面积公式可求也可用配方法
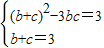 求得bc=2,直接代入面积公式可求
求得bc=2,直接代入面积公式可求解答:解:(Ⅰ)f(x)=
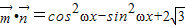
cosωx•sinωx=cos2ωx+
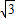 sin2ωx=
sin2ωx=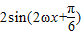
∵ω>0
∴函数f(x)的周期T=
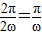 ,由题意可知
,由题意可知 ,
,解得0<ω≤1,即ω的取值范围是{ω|0<ω≤1}
(Ⅱ)由(Ⅰ)可知ω的最大值为1,
∴
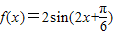
∵f(A)=1
∴
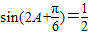
而
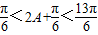 π
π∴2A+
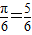 π
π∴A=
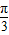
由余弦定理知cosA=
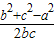
∴b2+c2-bc=3,又b+c=3
联立解得
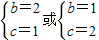
∴S△ABC=
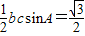
(或用配方法∵
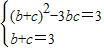
∴bc=2
∴
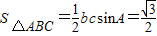 .
.点评:本题综合考查了向量的数量积的坐标表示,由函数的部分图象的性质求解函数的解析式,正弦函数的周期公式,由三角函数值求解角,余弦定理及三角形的面积公式等知识的综合,综合的知识比较多,解法灵活,要求考生熟练掌握基础知识并能灵活运用知识进行解题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|