题目内容
(1)已知a∈R,函数f(x)=x2(x-a),若f′(1)=1.求a的值并求曲线y=f(x)在点(1,f(1))处的切线方程y=g(x);
(2)已知函数f(x)=
的图象在点(2,f(2))处的切线方程为y=2.求a,b的值及f(x)的单调区间.
(2)已知函数f(x)=
| ax2 | 2x+b |
分析:(1)求函数导数,由f′(1)=1,得a的值,然后利用导数的几何意义求切线方程.
(2)利用切线方程,求a,b的值.
(2)利用切线方程,求a,b的值.
解答:解:(1)因为f(x)=x2(x-a),所以f'(x)=3x2-ax,若f'(1)=1,则3-a=1,解得a=2.
所以f(1)=1-a=1-2=-1,所以对应的切线方程为y-(-1)=x-1,所以y=x-2,即y=g(x)=x-2.
(2)因为函数f(x)=
的导数为f′(x)=
=
,
因为函数在点(2,f(2))处的切线方程为y=2,所以f(2)=2且f'(2)=0,
即:
,解得a=1,b=-2.
所以f′(x)=
=
,f(x)=
,函数的定义域为{x|x≠1}.
由f'(x)>0得,x>2或x<0,此时函数单调递增.
由f'(x)<0得,0<x<2且x≠1,此时函数单调递减.
故函数的递增区间为(2,+∞)和(-∞,0).
函数的递减区间为(0,1)和(1,2).
所以f(1)=1-a=1-2=-1,所以对应的切线方程为y-(-1)=x-1,所以y=x-2,即y=g(x)=x-2.
(2)因为函数f(x)=
| ax2 |
| 2x+b |
| 2ax2+2abx |
| (2x+b)2 |
| 2ax(x+b) |
| (2x+b)2 |
因为函数在点(2,f(2))处的切线方程为y=2,所以f(2)=2且f'(2)=0,
即:
|
所以f′(x)=
| 2x(x-2) |
| (2x-2)2 |
| x(x-2) |
| 2(x-1)2 |
| x2 |
| 2x-2 |
由f'(x)>0得,x>2或x<0,此时函数单调递增.
由f'(x)<0得,0<x<2且x≠1,此时函数单调递减.
故函数的递增区间为(2,+∞)和(-∞,0).
函数的递减区间为(0,1)和(1,2).
点评:本题主要考查导数的几何意义,利用导数求出切线斜率是解决本题的关键,考查学生的运算能力.

练习册系列答案
相关题目
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a-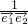 是偶函数.
是偶函数. =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a- 是偶函数.
是偶函数.