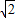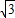Question

设A，B为圆x²+y²=1上两点，O为坐标原点（A，O，B不共线）
（1）求证：

OA

+

OB

与

OA

-

OB

垂直．
（2）当∠xOA=

π

4

，∠xOB=θ，θ∈(-

π

4

，

π

4

)且

OA

•

OB

=

3

5

时，求sinθ的值．

Answer 1

分析：（1）由已知中A，B为圆x²+y²=1上两点，O为坐标原点（A，O，B不共线），可得|

OA

|=|

OB

|=1，进而证得

OA

+

OB

与

OA

-

OB

的数量积为0，得到两个向量垂直．
（2）由∠xOA=

π

4

，∠xOB=θ，θ∈(-

π

4

，

π

4

)，可得A，B坐标，进而根据

OA

•

OB

=

3

5

，结合同角三角函数的基本关系和两角差的正弦公式，得到答案．

解答：（1）证明：∵A，B为圆x²+y²=1上两点，O为坐标原点
∴|

OA

|=|

OB

|=1，
又∵（

OA

+

OB

）•（

OA

-

OB

）
=

OA

2-

OB

2
=|

OA

|2-|

OB

|2
=1-1=0
∴

OA

+

OB

⊥

OA

-

OB

…（4分）
（2）解：∵∠xOA=

π

4

，∠xOB=θ，θ∈(-

π

4

，

π

4

)
∴A(cos

π

4

，sin

π

4

)，B(cosθ，sinθ)
∴

OA

•

OB

=cos

π

4

cosθ+sin

π

4

sinθ=sin(

π

4

+θ)=

3

5

…（8分）
∵θ∈(-

π

4

，

π

4

)
∴θ+

π

4

∈(0，

π

2

)
∴cos(θ+

π

4

)=

4

5

…（10分）
sinθ=sin(θ+

π

4

-

π

4

)=sin(θ+

π

4

)cos

π

4

-cos(θ+

π

4

)sin

π

4

=-

2

10

点评：本题考查的知识点是用向量的数量积判断两个向量的垂直关系，平面向量的数量积运算，是向量与三角函数的综合应用，难度为中档．