题目内容
已知a>0,数列{an}满足a1=a,an+1=a+ ,n=1,2,…。
,n=1,2,…。
(1)已知数列{an}极限存在且大于零,求A=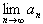 (将A用a表示);
(将A用a表示);
(2)设bn=an-A,n=1,2,…,证明: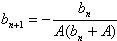 ;
;
(3)若|bn|≤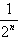 对n=1,2,…都成立,求a的取值范围。
对n=1,2,…都成立,求a的取值范围。
 ,n=1,2,…。
,n=1,2,…。(1)已知数列{an}极限存在且大于零,求A=
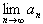 (将A用a表示);
(将A用a表示);(2)设bn=an-A,n=1,2,…,证明:
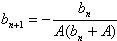 ;
;(3)若|bn|≤
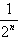 对n=1,2,…都成立,求a的取值范围。
对n=1,2,…都成立,求a的取值范围。解:(1)由 存在,且
存在,且 ,对
,对 两边取极限得
两边取极限得
 ,解得
,解得
又
∴ 。
。
(2)由 得
得
∴
即 对n=1,2,3,…都成立。
对n=1,2,3,…都成立。
(3)令 ,得
,得
∴
∴ ,解得
,解得
现证明当 时,
时, 对n=1,2,3,…都成立
对n=1,2,3,…都成立
(i)当n=1时结论成立(已验证)
(ii)假设当n=k(k≥1)时结论成立,即
那么
故只须证明 ,即证
,即证 对
对 成立
成立
由于
而当 时,
时,
∴
∴ ,即
,即
故当 时,
时,
即n=k+1时结论成立
根据(i)和(ii)可知结论对一切正整数都成立
故 对n=1,2,3,…都成立的a的取值范围为
对n=1,2,3,…都成立的a的取值范围为 。
。
 存在,且
存在,且 ,对
,对 两边取极限得
两边取极限得 ,解得
,解得
又

∴
 。
。(2)由
 得
得
∴

即
 对n=1,2,3,…都成立。
对n=1,2,3,…都成立。(3)令
 ,得
,得
∴

∴
 ,解得
,解得
现证明当
 时,
时, 对n=1,2,3,…都成立
对n=1,2,3,…都成立(i)当n=1时结论成立(已验证)
(ii)假设当n=k(k≥1)时结论成立,即

那么

故只须证明
 ,即证
,即证 对
对 成立
成立由于

而当
 时,
时,
∴

∴
 ,即
,即
故当
 时,
时,
即n=k+1时结论成立
根据(i)和(ii)可知结论对一切正整数都成立
故
 对n=1,2,3,…都成立的a的取值范围为
对n=1,2,3,…都成立的a的取值范围为 。
。
练习册系列答案
相关题目
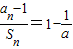 .数列{bn}中,bn=an•lgan.
.数列{bn}中,bn=an•lgan.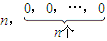 ;
;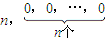 .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证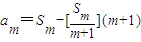 ,其中
,其中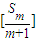 表示不超过
表示不超过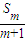 的最大整数.
的最大整数.