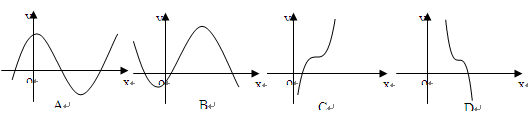
题目内容
定义在R上的函数f(x)满足f(x)-f(-x)=0,且对任意x,x∈[0,+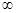 )(x
)(x x),都有
x),都有 ,则
,则
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
A
解析试题分析:定义在R上的函数f(x)满足f(x)-f(-x)=0,因此可知函数是奇函数,则由对任意x,x∈[0,+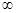 )(x
)(x x),都有
x),都有 ,则可知函数在x>0上单调递减,可知x<0时,单调递减,而f(-2)=-f(2),结合函数对称性可知f(3)<f(-2)<f(1),故选A.
,则可知函数在x>0上单调递减,可知x<0时,单调递减,而f(-2)=-f(2),结合函数对称性可知f(3)<f(-2)<f(1),故选A.
考点:函数的奇偶性
点评:对于函数中点比较大小可知,只要确定出函数的单调性,然后结合性质得到结论。属于基础题。

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
若函数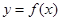 的定义域为
的定义域为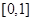 , 则下列函数中可能是偶函数的是 ( ).
, 则下列函数中可能是偶函数的是 ( ).
A.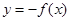 | B.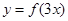 | C.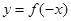 | D.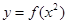 |
已知函数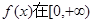 上是减函数,
上是减函数,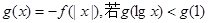 ,则x的取值
,则x的取值
范围是
A.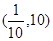 | B.(0,10) | C.(10,+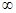 ) ) | D.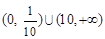 |
下面有四个结论:①偶函数的图像一定与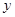 轴相交。②奇函数的图像不一定过原点。③偶函数若在
轴相交。②奇函数的图像不一定过原点。③偶函数若在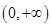 上是减函数,则在
上是减函数,则在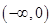 上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知a=lg3+lg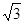 ,b=
,b= lg9,c=lg2,则a,b,c的大小关系是
lg9,c=lg2,则a,b,c的大小关系是
| A.b<a<c | B.c<a<b | C.a<b<c | D.c<b<a |
已知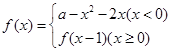 且函数
且函数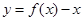 恰有3个不同的零点,则实数a的取值范围是( )
恰有3个不同的零点,则实数a的取值范围是( )
A.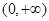 | B.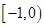 | C.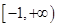 | D.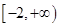 |
函数f(x)=ex- 的零点所在的区间是
的零点所在的区间是
A.(0, ) ) | B.( ,1) ,1) | C.(1, ) ) | D.( ,2) ,2) |
设 ,函数
,函数 的导函数是
的导函数是 ,且
,且 是奇函数,则
是奇函数,则 的值为
的值为
A. | B. | C. | D. |
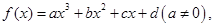 记
记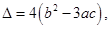 则当
则当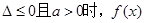 的大致图象为( )
的大致图象为( )