题目内容
设 为等差数列,
为等差数列, 为等比数列,且
为等比数列,且 ,若
,若 ,
数列
,
数列 的前三项依次为1,1,2
的前三项依次为1,1,2
(1)求 和
和 的通项公式;
的通项公式;
(2)在数列 中依次抽出第1,2,4…
中依次抽出第1,2,4… 项组成新数列
项组成新数列 ,写出
,写出 的通项公式;
的通项公式;
(3)设 求数列
求数列 的前
的前 项和
项和 .
.
【答案】
解:(1) ,
, ……………1 分
……………1 分
由 ,
, 得
得 解得:
解得: 或
或 (舍) ……………4 分
(舍) ……………4 分
所以, 的公差为
的公差为 ,
, ,
, 的通项公式为
的通项公式为
 的公比为2,
的公比为2,
 的通项公式为
的通项公式为 。
……………6 分
。
……………6 分
(2)
 ……………10分
……………10分
(3)

 (1) ……………12分
(1) ……………12分

 (2) ……………13分
(2) ……………13分
 得:
得:

即
 ……………15分
……………15分

练习册系列答案
相关题目
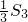 与
与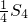 的等比中项为
的等比中项为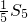 ,已知
,已知 与
与 的等比中项为
的等比中项为 ,已知
,已知 与
与 的等差中项为1.
的等差中项为1.