题目内容
【题目】在三角形ABC中,![]() ,D是垂足,则
,D是垂足,则![]() 推广到空间,三棱锥
推广到空间,三棱锥![]() 中,
中,![]() 面
面![]() 面
面![]() ,O为垂足,且O在三角形BCD内,则类似的结论为___________
,O为垂足,且O在三角形BCD内,则类似的结论为___________
【答案】![]()
【解析】
这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,AB⊥AC,点D是点A在BC边上的射影,则![]() ,我们可以类比这一性质,推理出若在三棱锥ABCD中,BA⊥平面ACD,点O是点A在平面BCD内的射影,即可得到答案
,我们可以类比这一性质,推理出若在三棱锥ABCD中,BA⊥平面ACD,点O是点A在平面BCD内的射影,即可得到答案
解:由已知在平面几何中,
若三角形ABC中,![]() ,D是垂足,
,D是垂足,
则![]() ,
,
我们可以类比这一性质,推理出:
若三棱锥![]() 中,
中,![]() 面
面![]() 面
面![]() ,O为垂足,
,O为垂足,
则![]() 。
。
证明:如图,连接DO并延长,交BC与点E,连接AE,BO,CO,
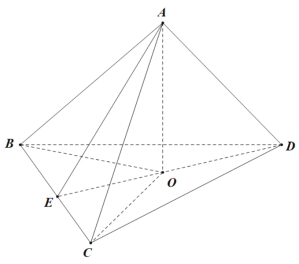
![]() 面
面![]() ,则
,则![]() ,
,
又![]() 面
面![]() ,则
,则![]() ,
,
所以在三角形![]() 中,
中,![]() ,
,![]() 是垂足,则
是垂足,则![]() ,
,
![]()
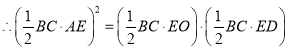 ,
,
![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目