Question

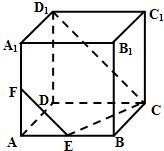
如图所示，在正方体ABCD-A₁B₁C₁D₁中，E是棱DD₁的中点，
(Ⅰ)求直线BE和平面ABB₁A₁所成的角的正弦值；
(Ⅱ)在棱C₁D₁上是否存在一点F，使B₁F∥平面A₁BE？证明你的结论．

Answer 1

解：设正方体的棱长为1，如图所示， 以为单位正交基底建立空间直角坐标系， (Ⅰ)依题意，得， 所以， 在正方形ABCD-A1B1C1D1中，因为AD⊥平面ABB1A1， 所以是平面ABB1A1的一个法向量， 设直线BE和平面ABB1A1所成的角为θ， 则， 即直线BE和平面ABB1A1所成的角的正弦值为。 (Ⅱ)依题意，得A1(0，0，1)，， 设n=(x，y，z)是平面A1BE的一个法向量， 则由，，得， 所以， 取z=2，得n=(2，1，2)； 设F是棱C1D1上的点，则F(t，1，1)(0≤t≤1)， 又B1(1，0，1)，所以， 而B1F平面A1BE， 于是=0 F为C1D1的中点． 这说明在棱C1D1上存在点F(C1D1的中点)，使B1F∥平面A1BE。