题目内容
已知定义在R上的二次函数 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数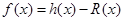 。
。
(I)求 的单调区间;
的单调区间;
(II)当 ≤
≤ 时,若
时,若 ,求
,求 的最小值;
的最小值;
(III)若二次函数 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数 图象上的点A(
图象上的点A( ),当
),当 时,探求函数
时,探求函数 图象上是否存在点B(
图象上是否存在点B( )(
)( ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。
(参考数据:e=2.71828…)
【答案】
(I)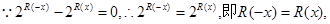
可得
又 在x=0时取得最小值0,
在x=0时取得最小值0,

令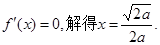
当x变化时,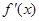 ,
,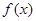 的变化情况如下表:
的变化情况如下表:
|
|
(0, |
|
( |
|
|
+ |
0 |
- |
|
|
增函数 |
极大值 |
减函数 |
所以,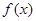 的单调递增区间是(0,
的单调递增区间是(0,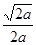 ),
),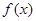 的单调递减区间是(
的单调递减区间是(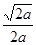 ,+
,+ )。
)。
(II) ≤
≤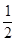 时,
时,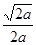 ≥1,
≥1,
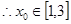 时,
时,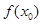 的最小值为
的最小值为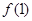 与
与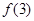 中的较小者. ……………………7分
中的较小者. ……………………7分
又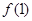
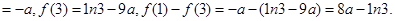
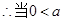 ≤
≤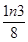 时,
时,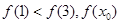 的最小值
的最小值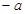 ;
;
当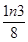
 时,
时, 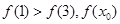 的最小值
的最小值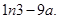 ……………………9分
……………………9分
(III)证明:若二次函数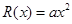 图象过(4,2)点,则
图象过(4,2)点,则 ,所以
,所以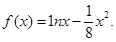
令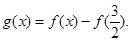
由(I)知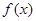 在(0,2)内单调递增,
在(0,2)内单调递增,
故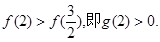 ……………………11分
……………………11分
取 则
则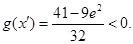
所以存在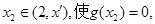
即存在
所以函数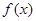 图象上存在点B(
图象上存在点B( )(
)( ),使A、B连线平行于x轴.
),使A、B连线平行于x轴.
【解析】略

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目

 满足
满足 ,且
,且 的最小值
的最小值 ,又函数
,又函数 。
。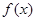 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若 ,求
,求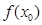 的最小值;
的最小值; ),
), 时,探求函数
时,探求函数 (
( )(
)( ),使
),使 、
、 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)