题目内容
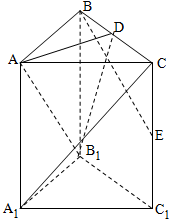 已知直三棱柱ABC-A1B1C1中,AB=AC,D为BC中点,E为CC1中点,侧面BCC1B1为正方形.
已知直三棱柱ABC-A1B1C1中,AB=AC,D为BC中点,E为CC1中点,侧面BCC1B1为正方形.(1)证明:A1C∥平面AB1D;
(2)证明:BE⊥AB1;
(3)设∠BAC=θ,若AB=
| 2 |
分析:(1)要证A1C∥平面AB1D,只需证明A1C∥OD即可;(2)要证BE⊥AB1,只要证BE⊥面AB1D,只要证BE垂直于平面中的两条相交直线;(3)因为AA1⊥面ABC,所以VA1-ABC=
•
•AB•AC•sinθ•AA1=
•2•sinθ•BC
从而VA1-ABC=
,利用导数法可求.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
从而VA1-ABC=
| 2 |
| 3 |
| cos3θ-cos2θ-cosθ+1 |
解答:证明: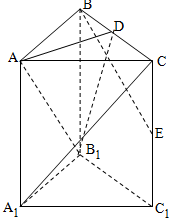 (1)连A1B交AB1于O,因为D为BC中点,所以A1C∥OD
(1)连A1B交AB1于O,因为D为BC中点,所以A1C∥OD
又∵A1C?面AB1D,OD⊆面AB1D∴A1C∥平面AB1D
(2)因为BCC1B1为正方形,D为BC中点,E为CC1中点,
所以△B1BD≌△BCE,所以∠EBC=∠BB1D
又因为∠BB1D+∠BDB1=900,所以∠EBC+∠BDB1=900
所以BE⊥B1D
因为AB=AC,D为BC中点,所以AD⊥BC
又因为面ABC⊥面BCC1B1,面ABC∩面BCC1B1=BC,AD⊆面ABC
所以AD⊥BCC1B1,所以AD⊥BE
又因为AD∩B1D=D,所以BE⊥面AB1D,所以BE⊥AB1
(3)因为AA1⊥面ABC,所以VA1-ABC=
•
•AB•AC•sinθ•AA1=
•2•sinθ•BC
在△ABC中,BC2=2+2-2•
•
•cosθ=4-4cosθ(0<θ<π)
所以VA1-ABC=
•2•sinθ•
=
=
令t=cosθ,f(t)=t3-t2-t+1,t∈(-1,1)
则f'(t)=3t2-2t-1,令f'(t)=0,得t=-
或t=1(舍去)
因为t∈(-1,-
)时,f'(t)>0,t∈(-
,1)时,f'(t)<0
所以f(t)在(-1,-
)递增,在(-
,1)递减,故max=f(-
)=
,此时cosθ=-
所以当cosθ=-
时,VA1-ABC取最大值
=
 (1)连A1B交AB1于O,因为D为BC中点,所以A1C∥OD
(1)连A1B交AB1于O,因为D为BC中点,所以A1C∥OD又∵A1C?面AB1D,OD⊆面AB1D∴A1C∥平面AB1D
(2)因为BCC1B1为正方形,D为BC中点,E为CC1中点,
所以△B1BD≌△BCE,所以∠EBC=∠BB1D
又因为∠BB1D+∠BDB1=900,所以∠EBC+∠BDB1=900
所以BE⊥B1D
因为AB=AC,D为BC中点,所以AD⊥BC
又因为面ABC⊥面BCC1B1,面ABC∩面BCC1B1=BC,AD⊆面ABC
所以AD⊥BCC1B1,所以AD⊥BE
又因为AD∩B1D=D,所以BE⊥面AB1D,所以BE⊥AB1
(3)因为AA1⊥面ABC,所以VA1-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
在△ABC中,BC2=2+2-2•
| 2 |
| 2 |
所以VA1-ABC=
| 1 |
| 6 |
| 4(1-cosθ) |
| 2 |
| 3 |
| (1-cos2θ)(1-cosθ) |
| 2 |
| 3 |
| cos3θ-cos2θ-cosθ+1 |
则f'(t)=3t2-2t-1,令f'(t)=0,得t=-
| 1 |
| 3 |
因为t∈(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
所以f(t)在(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 32 |
| 27 |
| 1 |
| 3 |
所以当cosθ=-
| 1 |
| 3 |
| 2 |
| 3 |
|
8
| ||
| 27 |
点评:本题主要考查空间线面位置关系,线面相互转化是关键,应熟练掌握相关性质与判定.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.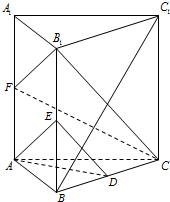 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.