题目内容
数列{an}的前n项和Sn,当n≥1时,Sn+1是an+1与Sn+1+k的等比中项(k≠0).(1)求证:对于
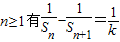 ;
;(2)设
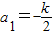 ,求Sn;
,求Sn;(3)对n≥1,试证明:S1S2+S2S3+…+SnSn+1

【答案】分析:(1)由题意知Sn+12=(Sn+1-Sn)(Sn+1+k),-Sn+1Sn+k(Sn+1-Sn)=0,等式两边同除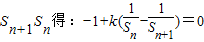
由此可知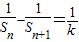 .
.
(2)由(1)知: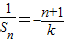 ,由此可知
,由此可知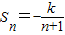 .
.
(3)S1S2+S2S3+…+SnSn+1=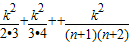 =
=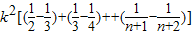 =
=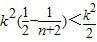 .
.
解答:证明:(1)由Sn+12=an+1•(Sn+1+k)而an+1=Sn+1-Sn
∴Sn+12=(Sn+1-Sn)(Sn+1+k)
∴-Sn+1Sn+k(Sn+1-Sn)=0
等式两边同除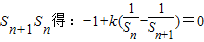
∴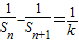 ;(4分)
;(4分)
(2)由(1)知: 为首项,
为首项,
以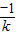 为公差的等差数列,
为公差的等差数列,
∴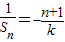
∴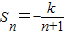 ;(8分)
;(8分)
(3)S1S2+S2S3+…+SnSn+1
=
=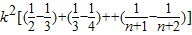
=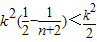 .(12分)
.(12分)
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
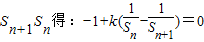
由此可知
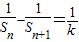 .
.(2)由(1)知:
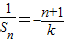 ,由此可知
,由此可知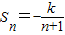 .
.(3)S1S2+S2S3+…+SnSn+1=
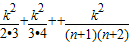 =
=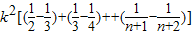 =
=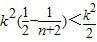 .
.解答:证明:(1)由Sn+12=an+1•(Sn+1+k)而an+1=Sn+1-Sn
∴Sn+12=(Sn+1-Sn)(Sn+1+k)
∴-Sn+1Sn+k(Sn+1-Sn)=0
等式两边同除
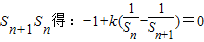
∴
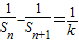 ;(4分)
;(4分)(2)由(1)知:
 为首项,
为首项,以
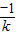 为公差的等差数列,
为公差的等差数列,∴
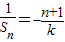
∴
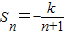 ;(8分)
;(8分)(3)S1S2+S2S3+…+SnSn+1
=

=
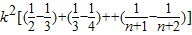
=
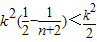 .(12分)
.(12分)点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目