题目内容
已知数列{an}的前n项和为Sn，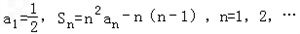
（1）证明：数列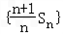
是等差数列，并求Sn；
（2）设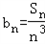
，求证：b1+b2+…+bn＜1．
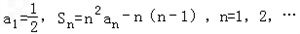
（1）证明：数列
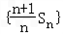是等差数列，并求Sn；（2）设
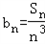，求证：b1+b2+…+bn＜1．证明：（1）由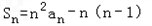
知，
当n≥2时：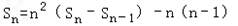
，
即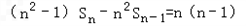
，
∴
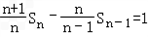，对n≥2成立．
又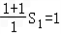
∴{
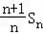}是首项为1，公差为1的等差数列．
∴
∴
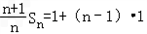
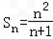
（2）
∴
=
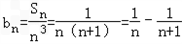
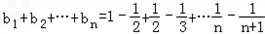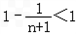
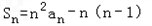知，当n≥2时：
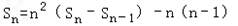，即
，∴
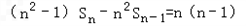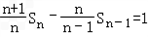，对n≥2成立． 又
∴{
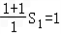
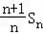}是首项为1，公差为1的等差数列．∴
∴
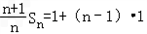
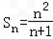
（2）
∴
=
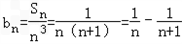
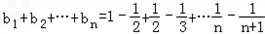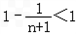
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn（a、b∈R），且S25=100，则a12+a14等于（ ）
| A、16 | B、8 | C、4 | D、不确定 |