题目内容
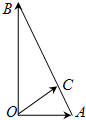 已知|
已知|| 0A |
| OB |
| 3 |
| OA |
| OB |
| OC |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:过点C做CE∥OA CF∥OB,得到两个三角形相似,根据三角形相似得到对应边成比例,把OE,OF都用OC来表示,代入比例式,求出OC的值,做出向量之间的关系.
解答:解:过点c做CE∥OA CF∥OB
设OC长度为a
有△CEB∽△AFC
∴
=
(1)
∵∠AOC=30°
则CF=
=OE
OF=CE=
∴BE=2
-
AF=2-
代入(1)中化简整理可解:a=
OF=
=
=
OA OE=
=
=
OB,
∴
=
+
=
+
故选B.
设OC长度为a
有△CEB∽△AFC
∴
| BE |
| CF |
| CE |
| AF |
∵∠AOC=30°
则CF=
| a |
| 2 |
OF=CE=
| ||
| 2 |
∴BE=2
| 3 |
| a |
| 2 |
| ||
| 2 |
代入(1)中化简整理可解:a=
| 3 |
OF=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| a |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
∴
| OC |
| OE |
| OF |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
故选B.
点评:本题考查平面向量基本定理及其意义,本题解题的关键是构造平行四边形,利用平行四边形法则来解题,本题是一个易错题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目