题目内容
已知不等式 的解集为
的解集为 ,
,
(1)求 的值;
的值;
(2)(文科做)解关于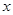 的不等式:
的不等式:
(2)(理科做)解关于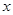 的不等式:
的不等式: .
.
(1)m+2n=7
(2)(文科做)a<-3时,不等式的解集为 ;
;
a>-3时,不等式的解集为 ;
;
a=-3时,不等式的解集为
(2)(理科做)
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ,或
,或 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ,或
,或 .
.
解析试题分析:(1)由不等式 的解集为
的解集为 知
知
关于x的方程 的两根为-1和n,且
的两根为-1和n,且
由根与系数关系,得 ∴
∴ ,
,
∴ m+2n=7
(2)(文科做)由(1)知关于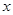 不等式
不等式 可以化为
可以化为 ,
,
即
故当-a>3,即a<-3时,不等式的解集为 ;
;
当-a<3,即a>-3时,不等式的解集为 ;
;
当-a=3,即a=-3时,不等式的解集为
(2)(理科做)解:原不等式化为 ,
,
① 当 时,原不等式化为
时,原不等式化为 ,解得
,解得 ;
;
② 当 时,原不等式化为
时,原不等式化为 ,且
,且 ,解得
,解得 ;
;
③ 当 时,原不等式化为
时,原不等式化为 ,且
,且 ,解得
,解得 或
或 ;
;
④ 当 时,原不等式化为
时,原不等式化为 ,解得
,解得 且
且 ;
;
⑤当 时,原不等式化为
时,原不等式化为 ,且
,且 ,解得
,解得 或
或 ;
;
综上所述,当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ,或
,或 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 ,或
,或 .
.
考点:含参数一元二次不等式的解法。
点评:中档题,含参数一元二次不等式的求解,首先应考虑因式分解法,讨论根的大小,写出解集。

练习册系列答案
相关题目
 的解集为
的解集为
 和
和 的值; (2)求不等式
的值; (2)求不等式 的解集.
的解集. 的解集为
的解集为 .
. ;
; .
. 的解集为
的解集为

 、
、 的值;
的值; .
.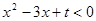 的解集为
的解集为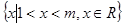
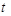 、
、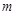 的值;
的值;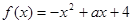 在区间
在区间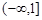 上递增,求关于
上递增,求关于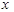 的不等式
的不等式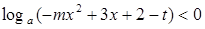 的解集。
的解集。 的解集为A,不等式
的解集为A,不等式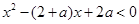 的解集为B
的解集为B ,求实数a的取值范围。
,求实数a的取值范围。